
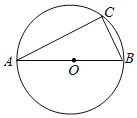
【题目】如图,在⊙O中,直径AB=10,tanA=![]() .
.
(1)求弦AC的长;
(2)D是AB延长线上一点,且AB=kBD,连接CD,若CD与⊙O相切,求k的值;
(3)若动点P以3cm/s的速度从A点出发,沿AB方向运动,同时动点Q以![]() cm/s的速度从B点出发沿BC方向运动,设运动时间为t (0<t<
cm/s的速度从B点出发沿BC方向运动,设运动时间为t (0<t<![]() ),连结PQ.当t为何值时,△BPQ为Rt△?
),连结PQ.当t为何值时,△BPQ为Rt△?
【答案】(1)5![]() ;(2)2;(3)
;(2)2;(3)![]() 秒或
秒或![]() 秒
秒
【解析】
(1)先利用特殊角的三角函数求出∠A,进而求出AC;
(2)先求出∠BOC=60°,进而得出∠D=30°,进而求出OD,即可求出BD,即可得出结论;
(3)先判断出点P在线段AB上,点Q在线段BC上,再分∠BQP=90°或∠BPQ=90°,最后用三角函数建立方程求解即可得出结论.
解:(1)∵⊙O的直径AB=10,
∴∠ACB=90°,
在Rt△ABC中,tanA=![]() ,
,
∴∠A=30°,
∴AC=ABcosA=10cos30°=10×![]() =5
=5![]() ,
,
即弦AC的长为5![]() ;
;
(2)如图1,连接OC,
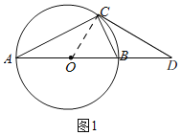
由(1)知,∠A=30°,
∴∠BOC=2∠A=60°,
∵CD是⊙O的切线,
∴∠OCD=90°,
∴∠D=90°﹣60°=30°,
∵OB=OC=![]() AB=5,
AB=5,
∴OD=2OC=10,
∴BD=OD﹣OB=10﹣5=5,
∵AB=kBD,
∴k=![]() =
=![]() =2,
=2,
即k的值为2;
(3)在Rt△ABC中,∵AB=10,∠A=30°,
∴BC=![]() AB=5,
AB=5,
由运动知,AP=3t,BQ=![]() ,
,
∵0<t<![]() ,
,
∴0<AP<10,0<BQ<5,
∴点P在线段AB上,点Q在线段BC上,
∵△BPQ为直角三角形,且∠ABC=90°﹣∠A=60°,
∴∠BQP=90°或∠BPQ=90°,
①当∠BQP=90°时,如图2,
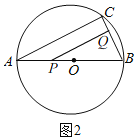
在Rt△BQP中,BP=AB﹣AP=10﹣3t,BQ=![]() t,∠ABC=60°,
t,∠ABC=60°,
∴cos∠ABC=![]() =
=![]() =
=![]() ,
,
∴t=![]() ,
,
②当∠BPQ=90°时,如图3,
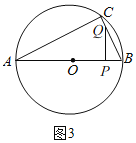
在Rt△BPQ中,cos∠ABC=![]() =
=![]() =
=![]() ,
,
∴t=![]() ,
,
即当t为![]() 秒或
秒或![]() 秒时,△BPQ为Rt△.
秒时,△BPQ为Rt△.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】下列每个图形都是由一些黑点和一些白点按一定的规律组成的.
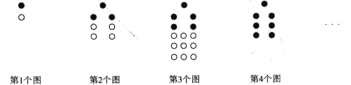
(1)根据规律,第4个图中有 个白点;第![]() 个图形中,白点和黑点总数的和为 (用
个图形中,白点和黑点总数的和为 (用![]() 表示,
表示,![]() 为正整数);
为正整数);
(2)有没有可能黑点比白点少2020个,如果有,求出此时![]() 的值;如果没有,请说明理由.
的值;如果没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在港口A的南偏东37°方向的海面上,有一巡逻艇B,A、B相距20海里,这时在巡逻艇的正北方向及港口A的北偏东67°方向上,有一渔船C发生故障.得知这一情况后,巡逻艇以25海里/小时的速度前往救援,问巡逻艇能否在1小时内到达渔船C处?
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin67°≈![]() ,cos67°≈
,cos67°≈![]() ,tan67°≈
,tan67°≈![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆慢车和一辆快车沿相同路线从A地到B地,所行驶的路程与时间的函数图象如图所示,下列说法正确的有( )
①快车追上慢车需6小时;
②慢车比快车早出发2小时;
③快车速度为46km/h;
④慢车速度为46km/h;
⑤AB两地相距828km;
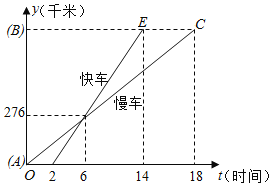
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
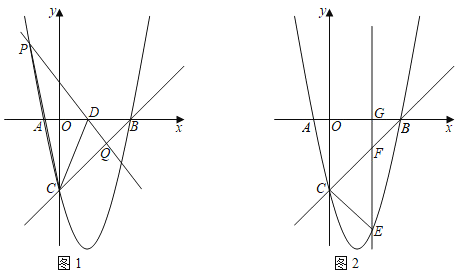
【题目】抛物线y=ax2+bx﹣5的图象与x轴交于A、B两点,与y轴交于点C,其中点A坐标为(﹣1,0),一次函数y=x+k的图象经过点B、C.
(1)试求二次函数及一次函数的解析式;
(2)如图1,点D(2,0)为x轴上一点,P为抛物线上的动点,过点P、D作直线PD交线段CB于点Q,连接PC、DC,若S△CPD=3S△CQD,求点P的坐标;
(3)如图2,点E为抛物线位于直线BC下方图象上的一个动点,过点E作直线EG⊥x轴于点G,交直线BC于点F,当EF+![]() CF的值最大时,求点E的坐标.
CF的值最大时,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:y=﹣![]() x与反比例函数y=
x与反比例函数y=![]() 的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2:
的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2:
(1)求反比例函数的表达式;
(2)将直线l1:y=﹣![]() x向上平移后的直线l2与反比例函数y=
x向上平移后的直线l2与反比例函数y=![]() 在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.
在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某社区今年准备新建一养老中心,其中规划建造三类养老专用房间共100间,这三类养老专用房间分别为单人间(1个养老床位),双人间(2个养老床位),三人间(3个养老床位),因实际需要,单人间房间数在10至30之间(包括10和30),且双人间的房间数是单人间的2倍,设规划建造单人间的房间数为![]() .
.
(1)根据题意,填写下表:
单人间的房间数 | 10 | … |
| … | 30 |
双人间的房间数 | _________ | … |
| … | 60 |
三人间的房间数 | 70 | … | _________ | … | _________ |
养老床位数 | 260 | … | _________ | … | _________ |
(2)若该养老中心建成后可提供养老床位200个,求![]() 的值;
的值;
(3)求该养老中心建成后最多提供养老床位多少个?最少提供养老床位多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于A(-1,0)和B(3,0)两点,与y轴交于点C,对称轴与x轴交于点E,点D为顶点,连接BD、CD、BC.
与x轴交于A(-1,0)和B(3,0)两点,与y轴交于点C,对称轴与x轴交于点E,点D为顶点,连接BD、CD、BC.

(1)求证△BCD是直角三角形;
(2)点P为线段BD上一点,若∠PCO+∠CDB=180°,求点P的坐标;
(3)点M为抛物线上一点,作MN⊥CD,交直线CD于点N,若∠CMN=∠BDE,请直接写出所有符合条件的点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com