
【题目】阅读材料:类比是数学中常用的数学思想.比如,我们可以类比多位数的加、减、乘、除的竖式运算方法,得到多项式与多项式的加、减、乘、除的运算方法.
例:
①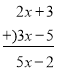 ②
②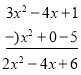
![]()
![]()
③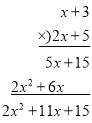 ④
④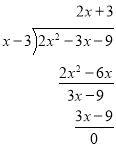
![]()
![]()
理解应用:
(1)请仿照上面的竖式方法计算:![]() ;
;
(2)已知两个多项式的和为![]() ,其中一个多项式为
,其中一个多项式为![]() ,请用竖式的方法求出另一个多项式.
,请用竖式的方法求出另一个多项式.
(3)已知一个长为![]() ,宽为
,宽为![]() 的矩形
的矩形![]() ,将它的长增加
,将它的长增加![]() ,宽增加
,宽增加![]() 得到一个新矩形
得到一个新矩形![]() ,且矩形
,且矩形![]() 的周长是矩形
的周长是矩形![]() 周长的
周长的![]() 倍(如图).同时,矩形
倍(如图).同时,矩形![]() 的面积和另一个边长为
的面积和另一个边长为![]() 的矩形
的矩形![]() 的面积相等,求
的面积相等,求![]() 的值和矩形
的值和矩形![]() 的另一边长.
的另一边长.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)m=-8,矩形C的另一边长为5x-10.
;(3)m=-8,矩形C的另一边长为5x-10.
【解析】
(1)根据多项式与多项式的乘法竖式的运算方法计算即可求解;
(2)根据多项式与多项式的减法竖式的运算方法计算即可求解;
(3)根据已知条件,求出面积,然后分解多项式即可.
解:(1)
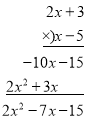
(2x+3)(x5)=2x27x15
(2)
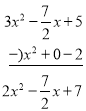
另一个多项式为:2x2![]() x+7
x+7
(3)∵矩形B的周长是A周长的3倍
∴2×(x+2+x2)×3=2×(x+10+x2+a)
∴a=4x8
所以矩形B的面积为:(x+8)(5x10)=5x2+30x80
矩形C的面积与B的面积相等,5x2+30x80=(x+8)(5x10),
故m=8,矩形C的另一边为5x10.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 轴,且直线l与抛物线
轴,且直线l与抛物线![]() 和y轴分别交于点A,B,C,点D为抛物线的顶点.若点E的坐标为
和y轴分别交于点A,B,C,点D为抛物线的顶点.若点E的坐标为![]() ,点A的横坐标为1.
,点A的横坐标为1.
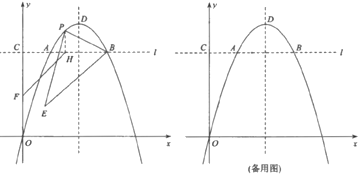
(1)线段AB的长度等于________;
(2)点P为线段AB上方抛物线上的一点,过点P作AB的垂线交AB于点H,点F为y轴上一点,当![]() 的面积最大时,求
的面积最大时,求![]() 的最小值;
的最小值;
(3)在(2)的条件下,删除抛物线![]() 在直线PH左侧部分图象并将右侧部分图象沿直线PH翻折,与抛物线在直线PH右侧部分图象组成新的函数M的图象.现有平行于FH的直线
在直线PH左侧部分图象并将右侧部分图象沿直线PH翻折,与抛物线在直线PH右侧部分图象组成新的函数M的图象.现有平行于FH的直线![]() ,若直线
,若直线![]() 与函数M的图象有且只有2个交点,求t的取值范围(请直接写出t的取值范围,无需解答过程).
与函数M的图象有且只有2个交点,求t的取值范围(请直接写出t的取值范围,无需解答过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市甲、乙、丙三个景区是人们节假日游玩的热点景区,某学校对九(5)班学生“五一”小长假随父母到这三个景区游玩的计划做了全面调查,调查分四个类别A:游三个景区:B:游两个景区;C:游一个景区:D:不到这三个景区游玩,现根据调查结果绘制了不完全的条形统计图和扇形统计图如下:
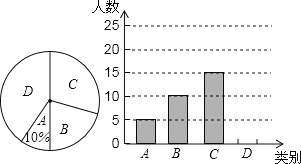
请结合图中信息解答下列问题:
(1)九(5)班现有学生人,并补全条形统计图;
(2)求在扇形统计图中表示“B类别”的扇形的圆心角的度数;
(3)根据调查显示,小刘和小何都选择“C类别”,求他俩游玩的恰好是同一景区的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
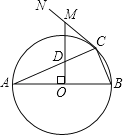
【题目】如图,AB是⊙O的直径,点C为⊙O上一点,CN为⊙O的切线,OM⊥AB于点O,分别交AC、CN于D、M两点.
(1)求证:MD=MC;
(2)若⊙O的半径为5,AC=4![]() ,求MC的长.
,求MC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了践行“金山银山,不如绿水青山”的环保理念,重外环保小组的孩子们参与社区公益活动——收集废旧电池,活动开展一个月后,经过统计发现,全组成员平均每人收集了![]() 颗废旧电池,其中,收集数量低于
颗废旧电池,其中,收集数量低于![]() 颗的同学平均每人收集了
颗的同学平均每人收集了![]() 颗,收集数量不低于
颗,收集数量不低于![]() 颗的同学平均每人收集了
颗的同学平均每人收集了![]() 颗,数学王老师发现,若每人再多收集
颗,数学王老师发现,若每人再多收集![]() 颗,则收集数量低于
颗,则收集数量低于![]() 颗的同学平均每人收集了
颗的同学平均每人收集了![]() 颗,收集数量不低于
颗,收集数量不低于![]() 颗的同学平均每人收集了
颗的同学平均每人收集了![]() 颗,并且,该环保小组的人数介于
颗,并且,该环保小组的人数介于![]() 至
至![]() 人.则该环保小组有__________人.
人.则该环保小组有__________人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O为△ABC的外接圆,BC为直径,点E在AB上,过点E作EF⊥BC,点G在FE的延长线上,且GA=GE.
(1)判断AG与⊙O的位置关系,并说明理由.
(2)若BA=8,∠B=37°,求直径BC的长(结果精确到0.01).

查看答案和解析>>
科目:初中数学 来源: 题型:
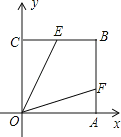
【题目】如图,在正方形OABC中,点B的坐标是(4,4),点E、F分别在边BC、BA上,OE=2![]() .若∠EOF=45°,则F点的纵坐标是( )
.若∠EOF=45°,则F点的纵坐标是( )
A.1B.![]() C.
C.![]() D.
D.![]() ﹣1
﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
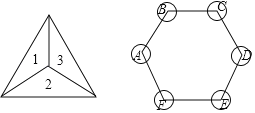
【题目】图①是一枚质地均匀的正四面体形状的骰子,每个面上分别标有数字1,2,3,4,图②是一个正六边形棋盘,现通过掷骰子的方式玩跳棋游戏,规则是:将这枚骰子掷出后,看骰子向上三个面(除底面外)的数字之和是几,就从图②中的A点开始沿着顺时针方向连续跳动几个顶点,第二次从第一次的终点处开始,按第一次的方法跳动.
(1)随机掷一次骰子,则棋子跳动到点C处的概率是
(2)随机掷两次骰子,用画树状图或列表的方法,求棋子最终跳动到点C处的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,光明中学一教学楼顶上竖有一块高为AB的宣传牌,点E和点D分别是教学楼底部和外墙上的一点(A,B,D,E在同一直线上),小红同学在距E点9米的C处测得宣传牌底部点B的仰角为67°,同时测得教学楼外墙外点D的仰角为30°,从点C沿坡度为1∶![]() 的斜坡向上走到点F时,DF正好与水平线CE平行.
的斜坡向上走到点F时,DF正好与水平线CE平行.
(1)求点F到直线CE的距离(结果保留根号);
(2)若在点F处测得宣传牌顶部A的仰角为45°,求出宣传牌AB的高度(结果精确到0.01).(注:sin67°≈0.92,tan67°≈2.36,![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com