
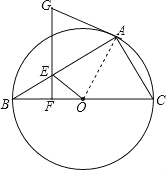
【题目】如图,已知⊙O为△ABC的外接圆,BC为直径,点E在AB上,过点E作EF⊥BC,点G在FE的延长线上,且GA=GE.
(1)判断AG与⊙O的位置关系,并说明理由.
(2)若BA=8,∠B=37°,求直径BC的长(结果精确到0.01).

【答案】(1)AG与⊙O相切,理由见解析;(2)10.02.
【解析】
试题(1)利用等腰三角形的性质结合三角形内角和定理得出∠BAO+∠GAE=90°,进而得出答案;
(2)利用锐角三角函数关系得出BC=![]() 即可得出答案.
即可得出答案.
试题解析:(1)AG与⊙O相切,
证明:如图 连接OA,
∵OA=OB,GA=GE,
∴∠ABO=∠BAO,∠GEA=∠GAE.
∵EF⊥BC,
∴∠BFE=90°.
∴∠ABO+∠BEF=90°.
又∵∠BEF=∠GEA,
∴∠GAE=∠BEF.
∴∠BAO+∠GAE=90°.
∴OA⊥AG,即AG与⊙O相切.
(2)∵BC为直径,
∴∠BAC=90°,
在Rt△BAC中,∠BAC=90°.
∵BA=8,∠B=37°,
∴BC=![]() ≈10.02.
≈10.02.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
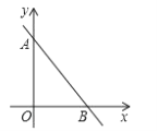
【题目】如图,在直角坐标系xOy中,O为坐标原点,直线AB分别与y轴,x轴交于A(0,4),B(3,0)两点.
(1)尺规作图:在x轴上求作一点C,使得△ABC是以![]() 为顶角的等腰三角形,并在图中标明相应字母;(保留作图痕迹,不写作法)
为顶角的等腰三角形,并在图中标明相应字母;(保留作图痕迹,不写作法)
(2)在(1)的条件下,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】党的十九大提出,建设生态文明是中华民族永续发展的千年大计,某同学参加“加强生态环境保护,建设美丽中国”手工大赛,他用一种环保材料制作A、B两种手工艺品,制作1件A种手工艺品和3件B种手工艺品需要环保材料5米,制作4件A种手工艺品和5件B种手工艺品需要环保材料13米,求制作一件A种手工艺品和1件B种手工艺品各需多少米环保材料?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“行千里,致广大”是重庆人民向大家发出的旅游邀请.如图,某建筑物上有一个旅游宣传语广告牌,小亮在![]() 处测得该广告牌顶部
处测得该广告牌顶部![]() 处的仰角为
处的仰角为![]() ,然后沿坡比为
,然后沿坡比为![]() 的斜坡
的斜坡![]() 行走
行走![]() 米至
米至![]() 处,在
处,在![]() 处测得广告牌底部
处测得广告牌底部![]() 处的仰角为
处的仰角为![]() ,已知
,已知![]() 与水平面
与水平面![]() 平行,
平行,![]() 与
与![]() 垂直,且
垂直,且![]() 米,则广告牌顶部
米,则广告牌顶部![]() 到
到![]() 的距离
的距离![]() 为( )(参考数据:
为( )(参考数据:![]() ,
,![]() ,
,![]() )
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:类比是数学中常用的数学思想.比如,我们可以类比多位数的加、减、乘、除的竖式运算方法,得到多项式与多项式的加、减、乘、除的运算方法.
例:
①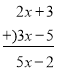 ②
②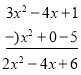
![]()
![]()
③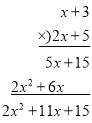 ④
④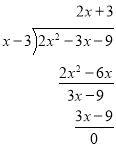
![]()
![]()
理解应用:
(1)请仿照上面的竖式方法计算:![]() ;
;
(2)已知两个多项式的和为![]() ,其中一个多项式为
,其中一个多项式为![]() ,请用竖式的方法求出另一个多项式.
,请用竖式的方法求出另一个多项式.
(3)已知一个长为![]() ,宽为
,宽为![]() 的矩形
的矩形![]() ,将它的长增加
,将它的长增加![]() ,宽增加
,宽增加![]() 得到一个新矩形
得到一个新矩形![]() ,且矩形
,且矩形![]() 的周长是矩形
的周长是矩形![]() 周长的
周长的![]() 倍(如图).同时,矩形
倍(如图).同时,矩形![]() 的面积和另一个边长为
的面积和另一个边长为![]() 的矩形
的矩形![]() 的面积相等,求
的面积相等,求![]() 的值和矩形
的值和矩形![]() 的另一边长.
的另一边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】林城市对教师试卷讲评课中学生参与的深度和广度进行评价,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中学生的参与情况,绘制了如图两幅不完整的统计图,请根据图中所给信息解答下列问题:
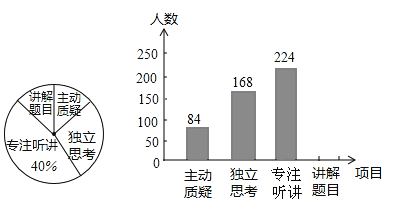
(1)在这次评价中,一共抽查了 名学生;
(2)请将条形统计图补充完整;
(3)如果全市有16万名初中学生,那么在试卷讲评课中,“独立思考”的学生约有多少万人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某中学九年级数学活动小组选定测量学校前面小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°.若斜坡FA的坡比i=1:![]() ,求大树的高度.(结果保留一位小数)参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,
,求大树的高度.(结果保留一位小数)参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,![]() 取1.73.
取1.73.

查看答案和解析>>
科目:初中数学 来源: 题型:
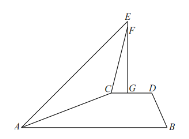
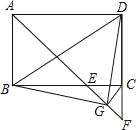
【题目】如图,在矩形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F,取EF的中点G,连接CG,BG,BD,DG,下列结论:
①BE=CD;
②∠DGF=135°;
③△BEG≌△DCG;
④∠ABG+∠ADG=180°;
⑤若![]() ,则3S△BDG=13S△DGF.
,则3S△BDG=13S△DGF.
其中正确的结论是_____.(请填写所有正确结论的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com