
����Ŀ��ij�мס��ҡ����������������ǽڼ���������ȵ㾰����ijѧУ�Ծţ�5����ѧ������һ��С�����游ĸ����������������ļƻ�����ȫ����飬������ĸ����A��������������B��������������C����һ��������D�������������������棬�ָ��ݵ����������˲���ȫ������ͳ��ͼ������ͳ��ͼ���£�
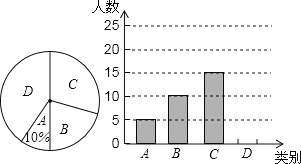
����ͼ����Ϣ����������⣺
��1���ţ�5��������ѧ���ˣ�����ȫ����ͳ��ͼ��
��2����������ͳ��ͼ�б�ʾ��B��𡱵����ε�Բ�ĽǵĶ�����
��3�����ݵ�����ʾ��С����С�ζ�ѡ��C��𡱣������������ǡ����ͬһ�����ĸ��ʣ�
���𰸡���1��50������������2��72�㣻��3��![]() .
.
��������
��1���������D������������ɽ�����ͳ��ͼ������������2����A��5�ˣ�ռ10%����������������̶����B���ռ�İٷ�������������B����������ε�Բ�ĽǵĶ�����
��3�����ȸ������⻭����״ͼ��Ȼ������״ͼ������еȿ��ܵĽ��������ͬʱѡ����C�����������������ø��ʹ�ʽ��⼴����ô𰸣�
�⣺��1����A��5�ˣ�ռ10%��
��ˣ�1�����ѧ���У�5��10%��50���ˣ���
D�ࣺ50��5��10��15��20���ˣ�����ͼ��
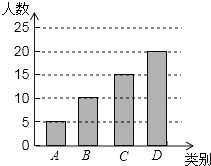 ��
��
�ʴ�Ϊ��50��
��2��������ͳ��ͼ�У���ʾ��B����������ε�Բ�ĽǵĶ���Ϊ��![]() ��360����72����
��360����72����
��3������״ͼ���£�
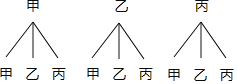
����״ͼ֪������9�ֵȿ��ܽ�����������������ǡ����ͬһ��������3�ֽ����
�������������ǡ����ͬһ�����ĸ���Ϊ![]() ��
��


 �ִʾ�ƪ��ͬ�����Ĵ��ϵ�д�
�ִʾ�ƪ��ͬ�����Ĵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��O�İ뾶Ϊ13����AB��CD��AB=24��CD=10�����ı���ACDB������ǣ�������
A.119B.289C.77��119D.119��289
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪һ��ֱ�߾�����C(��1��0)��D(0����2)��������ֱ������ƽ����x�ᡢy��ֱ��ڵ�B����A����DB��DC����ֱ��AB�ĺ�������ʽΪ_____��
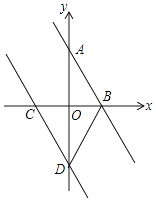
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��ʵ������ƶ����ij���������ķ����½������߲˴�����أ�����ֲA��B�����߲ˣ�����ֲ20ĶA���߲˺�30ĶB���߲ˣ�����Ͷ��36��Ԫ������ֲ30ĶA���߲˺�20ĶB���߲ˣ�����Ͷ��34��Ԫ��
��1����ֲA��B�����߲ˣ�ÿĶ����Ͷ�������Ԫ��
��2�������㣬��ֲA���߲�ÿĶ�ɻ���0.8��Ԫ����ֲB���߲�ÿĶ�ɻ���1.2��Ԫ�������100��Ԫ��ƶ��ȫ��������ֲ�������߲ˣ��ܻ���w��Ԫ������ֲA���߲�mĶ����w����m�ĺ�����ϵʽ��
��3���ڣ�2���������£���Ҫ��A���߲˵���ֲ�����������B���߲���ֲ�����2����������Ƴ��ܻ���������ֲ���������������ܻ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�Ƕ��κ���y��ax2+bx+cͼ���һ���֣�ͼ�����A����5��0�����Գ���Ϊֱ��x����2�������ĸ����ۣ���abc��0����4a��b��0��������B����3��y1����C��0��y2��Ϊ����ͼ���ϵ����㣬��y1��y2����a+b+c��0�����У���ȷ���۵ĸ����ǣ�������
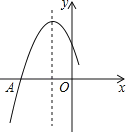
A.1B.2C.3D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʮ�Ŵ������������̬�������л�����������չ��ǧ���ƣ�ijͬѧ�μӡ���ǿ��̬�������������������й����ֹ�����������һ�ֻ�����������A��B�����ֹ���Ʒ������1��A���ֹ���Ʒ��3��B���ֹ���Ʒ��Ҫ��������5�ף�����4��A���ֹ���Ʒ��5��B���ֹ���Ʒ��Ҫ��������13�ף�������һ��A���ֹ���Ʒ��1��B���ֹ���Ʒ��������������ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������ABCD����M�DZ�BA�ӳ����ϵĶ���(�����A�غ�)����AM��AB����CBE�ɡ�DAMƽ�Ƶõ���������E��EH��AC��HΪ���㣬�������½��ۣ�
����Mλ�ñ仯��ʹ�á�DHC��60��ʱ��2BE��DM��
�����۵�M�˶����δ�������DM��![]() HM��
HM��
�����۵�M�˶����δ�����CHMһ������135�㣮������ȷ���۵����Ϊ(����)
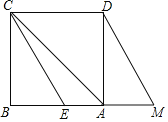
A.�٢�B.�٢�C.�ڢ�D.�٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����ϣ��������ѧ�г��õ���ѧ˼��.���磬���ǿ�����ȶ�λ���ļӡ������ˡ�������ʽ���㷽�����õ�����ʽ�����ʽ�ļӡ������ˡ��������㷽��.
����
��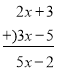 ��
��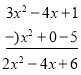
![]()
![]()
��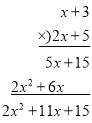 ��
��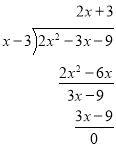
![]()
![]()
����Ӧ�ã�
��1��������������ʽ�������㣺![]() ��
��
��2����֪��������ʽ�ĺ�Ϊ![]() ������һ������ʽΪ
������һ������ʽΪ![]() ��������ʽ�ķ��������һ������ʽ.
��������ʽ�ķ��������һ������ʽ.
��3����֪һ����Ϊ![]() ����Ϊ
����Ϊ![]() �ľ���
�ľ���![]() �������ij�����
�������ij�����![]() ��������
��������![]() �õ�һ���¾���
�õ�һ���¾���![]() ���Ҿ���
���Ҿ���![]() ���ܳ��Ǿ���
���ܳ��Ǿ���![]() �ܳ���
�ܳ���![]() ������ͼ��.ͬʱ������
������ͼ��.ͬʱ������![]() ���������һ���߳�Ϊ
���������һ���߳�Ϊ![]() �ľ���
�ľ���![]() �������ȣ���
�������ȣ���![]() ��ֵ�;���
��ֵ�;���![]() ����һ�߳�.
����һ�߳�.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���֪AB��BC��10��AC��4![]() ��ADΪ��BC�ϵĸ��ߣ�PΪ��AD��һ�㣬����BP��EΪ�߶�BP��һ�㣬��D��P��E�����Բ����BC��F������EF��
��ADΪ��BC�ϵĸ��ߣ�PΪ��AD��һ�㣬����BP��EΪ�߶�BP��һ�㣬��D��P��E�����Բ����BC��F������EF��
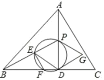
��1����AD�ij���
��2����֤����BEF�ס�BDP��
��3������DE����DP��3������DEPΪ����������ʱ����BF�ij���
��4���ѡ�DEP����ֱ��DP���۵õ���DGP����G���ڱ�AC�ϣ���DG��BP���ǡ�APG����PDG����GDC������ֱ�ΪS1��S2��S3����S1��S2��S3��ֵΪ�� ����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com