Question

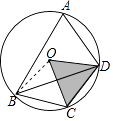
【题目】如图，四边形ABCD内接于⊙O，C为 的中点，若∠CBD=30°，⊙O的半径为12．
（1）求∠BAD的度数；
（2）求扇形OCD的面积．

Answer 1

【答案】
（1）解：∵C是为 的中点，

∴ =2 ，

∴∠BAD=∠COD，

∵ = ，

∴∠COD=2∠CBD，

∴∠BAD=2∠CBD，

∵∠CBD=30°，

∴∠BAD=60°

（2）解：∵ = ，

∴∠COD=2∠CBD，

∵∠CBD=30°，

∴∠COD=60°，

则S扇形OCD= =24π．

【解析】（1）根据题意可得 =2 ，进而可得∠BAD=∠COD，∠BAD=2∠CBD，再由条件∠CBD=30°可得∠BAD的度数；（2）根据圆周角定理可得∠COD=60°，再根据扇形的面积公式可得答案．
【考点精析】掌握圆内接四边形的性质和扇形面积计算公式是解答本题的根本，需要知道把圆分成n(n≥3):1、依次连结各分点所得的多边形是这个圆的内接正n边形2、经过各分点作圆的切线，以相邻切线的交点为顶点的多边形是这个圆的外切正n边形；在圆上，由两条半径和一段弧围成的图形叫做扇形；扇形面积S=π（R2-r2）．