
【题目】如图,在△ABC 中,AB=AC,∠A=36°,BD 平分∠ABC 交 AC 于 D,CE 平分∠ACB 交 BD 于 E,图中 等腰三角形的个数是( )

A.3 个B.4 个C.5 个D.6 个
【答案】C
【解析】
在△ABC中,AB=AC,∠A=36°,可得∠ABC=∠ACB=72°,根据BD和CE是角平分线得出∠ABD=∠EBC=∠ACE=∠ECB=36°,再根据三角形的外角定理得出:∠CDE=∠CED=72°,再根据上面等腰三角形的判定定理判断即可.
∵AB=AC,∠A=36°
∴△ABC是等腰三角形,且∠ABC=∠ACB=![]()
又∵BD 平分∠ABC,CE 平分∠ACB
∴∠ABD=∠EBC=∠ACE=∠ECB=36°
∴△EBC是等腰三角形
∵∠ABD=∠A=36°
∴△ABD是等腰三角形
∵∠CED=∠ECB+∠EBC=72°且∠CDE=∠ABD+∠A=72°
∴∠CED=∠CDE=∠ACB=72°
∴△EDC和△BCD是等腰三角形
综上所述共有5个等腰三角形.
故选:C.


科目:初中数学 来源: 题型:
【题目】如图,数轴上每相邻两点相距一个单位长度,点A、B、C、D是这些点中的四个,且对应的位置如图所示,它们对应的数分别是a、b、c、d.
![]()
(1)若c与d互为相反数,则a________;
(2)若d2b8,那么点C对应的数是________;
(3)若abcd0,ab0求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)甲、乙、丙、丁四人做传球游戏:第一次由甲将球随机传给乙、丙、丁中的某一人,从第二次起,每一次都由持球者将球再随机传给其他三人中的某一人.求第二次传球后球回到甲手里的概率.(请用“画树状图”的方式给出分析过程)
(2)如果甲跟另外n(n≥2)个人做(1)中同样的游戏,那么,第三次传球后球回到甲手里的概率是 (请直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
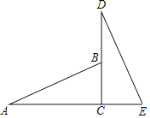
【题目】如图,已知C是线段AE上一点,![]() ,
,![]() ,B是CD上一点,CB=CE
,B是CD上一点,CB=CE
![]() 1
1![]() 求证:
求证:![]() ≌
≌![]() ;
;
![]() 2
2![]() 若∠E=65°,求∠A的度数;
若∠E=65°,求∠A的度数;
![]() 3
3![]() 若AE=11,BC=3,求BD的长,
若AE=11,BC=3,求BD的长,![]() 直接写出结果
直接写出结果![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点![]() 、
、![]() 分别为数轴上的两点,点
分别为数轴上的两点,点![]() 对应的数是
对应的数是![]() ,点
,点![]() 对应的数是
对应的数是![]() .现在有一动点
.现在有一动点![]() 从
从![]() 点出发,以每秒
点出发,以每秒![]() 个单位长度的速度向右运动,同时另一动点
个单位长度的速度向右运动,同时另一动点![]() 从点
从点![]() 出发以每秒
出发以每秒![]() 个单位长度的速度向左运动.
个单位长度的速度向左运动.
![]()
(1)与![]() 、
、![]() 两点相等的点
两点相等的点![]() 所对应的数是_________.
所对应的数是_________.
(2)两动点![]() 、
、![]() 相遇时所用时间为________秒;此时两动点所对应的数是_________.
相遇时所用时间为________秒;此时两动点所对应的数是_________.
(3)动点![]() 所对应的数是
所对应的数是![]() 时,此时动点
时,此时动点![]() 所对应的数是_________.
所对应的数是_________.
(4)当动点![]() 运动
运动![]() 秒钟时,动点
秒钟时,动点![]() 与动点
与动点![]() 之的距离是________单位长度.
之的距离是________单位长度.
(5)经过________秒钟,两动点![]() 、
、![]() 在数轴上相距
在数轴上相距![]() 个单位长度.
个单位长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为选派一名学生参加全市实践活动技能竞赛,A.B两位同学在学校实习基地现场进行加工直径为20mm的零件的测试,他俩各加工的10个零件的相关数据依次如下图表所示(单位:mm)
平均数 | 方差 | 完全符合要求个数 | |
A | 20 | 0.026 | 2 |
B | 20 | SB2 |
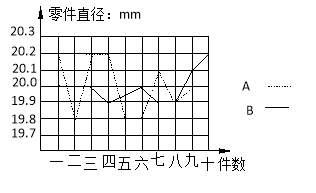
根据测试得到的有关数据,试解答下列问题:
⑴ 考虑平均数与完全符合要求的个数,你认为 的成绩好些;
⑵ 计算出SB2的大小,考虑平均数与方差,说明谁的成绩好些;
⑶ 考虑图中折线走势及竞赛中加工零件个数远远超过10个的实际情况,你认为派谁去参赛较合适?说明你的理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】党的十九大提出,建设生态文明是中华民族永续发展的千年大计,某同学参加“加强生态环境保护,建设美丽中国”手工大赛,他用一种环保材料制作A、B两种手工艺品,制作1件A种手工艺品和3件B种手工艺品需要环保材料5米,制作4件A种手工艺品和5件B种手工艺品需要环保材料13米,求制作一件A种手工艺品和1件B种手工艺品各需多少米环保材料?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC 中,∠ABC 和∠ACB 的角平分线交于点 M.
(1)若∠ABC=40°,∠ACB=60°,求∠BMC 的度数;
(2)∠BMC 可能是直角吗?作出判断,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,DE是边AB的垂直平分线,交AB于E、交AC于D,连接BD.
(1)若∠ABC=∠C,∠A=40°,求∠DBC的度数;
(2)若AB=AC,且△BCD的周长为18cm,△ABC的周长为30cm,求BE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com