
【题目】如图,已知点![]() 、
、![]() 分别为数轴上的两点,点
分别为数轴上的两点,点![]() 对应的数是
对应的数是![]() ,点
,点![]() 对应的数是
对应的数是![]() .现在有一动点
.现在有一动点![]() 从
从![]() 点出发,以每秒
点出发,以每秒![]() 个单位长度的速度向右运动,同时另一动点
个单位长度的速度向右运动,同时另一动点![]() 从点
从点![]() 出发以每秒
出发以每秒![]() 个单位长度的速度向左运动.
个单位长度的速度向左运动.
![]()
(1)与![]() 、
、![]() 两点相等的点
两点相等的点![]() 所对应的数是_________.
所对应的数是_________.
(2)两动点![]() 、
、![]() 相遇时所用时间为________秒;此时两动点所对应的数是_________.
相遇时所用时间为________秒;此时两动点所对应的数是_________.
(3)动点![]() 所对应的数是
所对应的数是![]() 时,此时动点
时,此时动点![]() 所对应的数是_________.
所对应的数是_________.
(4)当动点![]() 运动
运动![]() 秒钟时,动点
秒钟时,动点![]() 与动点
与动点![]() 之的距离是________单位长度.
之的距离是________单位长度.
(5)经过________秒钟,两动点![]() 、
、![]() 在数轴上相距
在数轴上相距![]() 个单位长度.
个单位长度.
【答案】30; 20; 40; 52; 25; 12或28.
【解析】
(1)根据数轴上A、B两点所表示的数为a、b,则AB的中点所表示的数可以用公式![]() 计算;
计算;
(2)设两动点相遇时间为t秒,P、Q两点运动的路程之和为总路程,列方程求解即可;用80-2t即可求得此时两动点对应的数;
(3)先求出动点P对应的点是22时运动的时间,再根据Q和P运动时间相等计算Q点运动路程,进而求得点Q对应的数;
(4)根据题意P、Q两点25秒运动的路程和减去总路程就是PQ两点间的距离;
(5)根据题意,分两种情况进行解答,即:①相遇前相距40个单位长度,②相遇后相距40个单位长度,分别列方程求解即可.
解:(1)AB的中点C所对应的数为:![]()
(2)设两动点相遇时间为t秒,(2+3)t=80-(-20) 解得:t=20(秒)
80-2t=80-2×20=40,或-20+3×20=40
∴此时两动点所对应的点为40;
(3)22-(-20)=42, 80-42÷3×2=52
∴动点![]() 所对应的数是
所对应的数是![]() 时,此时Q所对应的数为52;
时,此时Q所对应的数为52;
(4)∵20秒相遇,∴(2+3) ×25-[80-(-20)]=25
(5)P、Q两点相距40个单位长度,分两种情况
AB=80-(-20)=100
①相遇前,(100-40) ÷(3+2)=60÷5=12(秒)
②相遇后,(100+40)÷(2+3)=140÷5 =28(秒)
∴经过12或28秒钟,两动点![]() 、
、![]() 在数轴上相距
在数轴上相距![]() 个单位长度.
个单位长度.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图所示的坐标系中,△ABC的三个顶点的坐标依次为A(﹣1,2),B(﹣4,1),C(﹣2,﹣2)
(1)请写出△ABC关于x轴对称的点A1、B1、C1的坐标;
(2)请在这个坐标系中作出△ABC关于y轴对称的△A2B2C2;
(3)计算:△A2B2C2的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
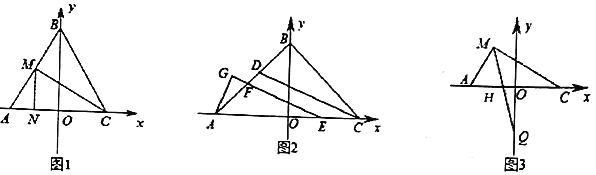
【题目】在平面直角坐标系中,已知![]() ,
,![]() ,
,![]() .
.
(1)如图1,若![]() ,
,![]() 于点
于点![]() ,
,![]() 轴交
轴交![]() 于点
于点![]() ,则
,则![]() _____.
_____.
(2)如图2,若![]() ,
,![]() 的平分线
的平分线![]() 交
交![]() 于点
于点![]() ,过
,过![]() 上一点作
上一点作![]() ,交
,交![]() 于点
于点![]() ,
,![]() 是
是![]() 的高,探究
的高,探究![]() 与
与![]() 的数量关系;
的数量关系;
(3)如图3,在(1)的条件下,![]() 上点
上点![]() 满足
满足![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
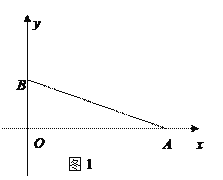
【题目】如图,在平面直角坐标系中,已知点A、B的坐标分别是A(6,0)、B(0,2),在AB的右上方有一点C,使△ABC是以AB为斜边的直角三角形.
(1)若点C坐标为(x,y),请在图1中作一点C(点A除外),使x+y=6;
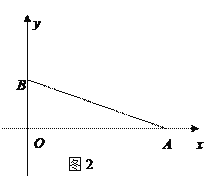
(2)设点C坐标为(x,y),请在图2中作一点C,使x+y的值最大,并求出x+y的最大值.
请利用没有刻度的直尺和圆规作出符合条件的点C.(注:不写作法,保留作图痕迹,对图中涉及到的点用字母进行标注)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们都知道![]() 表示
表示![]() 与
与![]() 之差的绝对值,实际上也可理解为
之差的绝对值,实际上也可理解为![]() 与
与![]() 两数在数轴上所对的两点之间的距离,试探索:
两数在数轴上所对的两点之间的距离,试探索:
(1)求![]() __________.
__________.
(2)找出所有符合条件的整数![]() ,使得
,使得![]() .满足条件的所有整数值有___________
.满足条件的所有整数值有___________
(3)由以上探索,猜想对于任何有理数![]() ,
,![]() 是否有最大值或最小值?如果有最大值或最小值是多少?
是否有最大值或最小值?如果有最大值或最小值是多少?![]() 有最__________(填“最大”或“最小”)值是__________.
有最__________(填“最大”或“最小”)值是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,AB=AC,∠A=36°,BD 平分∠ABC 交 AC 于 D,CE 平分∠ACB 交 BD 于 E,图中 等腰三角形的个数是( )

A.3 个B.4 个C.5 个D.6 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线 PQ 上有一点 O,点 A 为直线外一点,连接 OA,在直线 PQ 上找一点 B,使得△AOB 是等腰三角形,这样的点 B 有_____个.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明设计的“分别以两条已知线段为腰和底边上的高作等腰三角形”的尺规作图过程.
已知:线段 a, b.
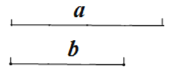
求作:等腰△ABC,使线段 a 为腰,线段 b 为底边 BC 上的高. 作法:如图,
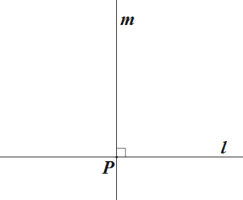
①画直线 l,作直线 m⊥l,垂足为 P;
②以点 P 为圆心,线段 b 的长为半径画弧,交直线 m 于点 A;
③以点 A 为圆心,线段 a 的长为半径画弧,交直线 l 于 B,C 两点;
④分别连接 AB, AC;
所以△ABC 就是所求作的等腰三角形. 根据小明设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵ = ,
∴△ABC 为等腰三角形( )(填推理的依据).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在抗洪抢险中,人民解放军的冲锋舟沿南北方向的河流抢救灾民.约定向北为正方向,某冲锋舟从 A 地出发,到达B地的一趟的航程记录如下(单位:千米):
![]()
(1)B地在A地的何方?相距多少千米?
(2)若冲锋舟每千米耗油![]() 升,油箱的容量为29 升,则途中至少需要补充多少升油?
升,油箱的容量为29 升,则途中至少需要补充多少升油?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com