
【题目】同学们都知道![]() 表示
表示![]() 与
与![]() 之差的绝对值,实际上也可理解为
之差的绝对值,实际上也可理解为![]() 与
与![]() 两数在数轴上所对的两点之间的距离,试探索:
两数在数轴上所对的两点之间的距离,试探索:
(1)求![]() __________.
__________.
(2)找出所有符合条件的整数![]() ,使得
,使得![]() .满足条件的所有整数值有___________
.满足条件的所有整数值有___________
(3)由以上探索,猜想对于任何有理数![]() ,
,![]() 是否有最大值或最小值?如果有最大值或最小值是多少?
是否有最大值或最小值?如果有最大值或最小值是多少?![]() 有最__________(填“最大”或“最小”)值是__________.
有最__________(填“最大”或“最小”)值是__________.
【答案】(1)7;(2)-3,-2,-1,0,1,2;(3)最小,3
【解析】
(1)直接去括号,再按照去绝对值的方法去掉绝对值就可以了;
(2)要求x的整数值可以进行分段计算,令x+3=0或x-2=0时,分为3段进行计算,最后确定x的值.
(3)根据(2)方法去绝对值,分为3种情况去绝对值符号,计算三种不同情况的值,最后讨论得出最小值.
解:(1)原式=|5+2|=7.
故答案为:7;
(2)令x+3=0或x-2=0时,则x=-3或x=2.
当x<-3时,-(x+3)-(x-2)=5,
-x-3-x+2=5,解得x=-3(范围内不成立)
当-3≤x≤2时,(x+3)-(x-2)=5,
x+3-x+1=4,0x=0,x为任意数,
则整数x=-3,-2,-1,0,1,
当x>2时,(x+3)+(x-2)=5,
x=2(范围内不成立) .
综上所述,符合条件的整数x有:-3,-2,-1,0,1,2.
故答案为:-3,-2,-1,0,1,2;
(3)由(2)的探索猜想,对于任何有理数x,![]() 有最小值为3,
有最小值为3,
令x-3=0或x-6=0时,则x=3,x=6
当x<3时,-(x-3)-(x-6)=-2x+3﹥3
当3≤x≤6时,x-3-(x-6)=3,
当x>6时,x-3+x-6=2x-9>3
∴对于任何有理数x,![]() 有最小值为3
有最小值为3


科目:初中数学 来源: 题型:
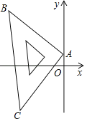
【题目】把一个等腰直角三角板放在黑板上画好了的平面直角坐标系内,如图,已知直角顶点A的坐标为(0,1),另一个顶点B的坐标为(﹣5,5),则点C的坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD与正方形CEFG,M是AF的中点,连接DM,EM.
(1)如图1,点E在CD上,点G在BC的延长线上,请判断DM,EM的数量关系与位置关系,并直接写出结论;
(2)如图2,点E在DC的延长线上,点G在BC上,(1)中结论是否仍然成立?请证明你的结论;
(3)将图1中的正方形CEFG绕点C旋转,使D,E,F三点在一条直线上,若AB=13,CE=5,请画出图形,并直接写出MF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小欢和小丽都十分喜欢唱歌.她们两人一起参加学校的文艺汇演.在汇演前,主持人让她们自己确定出场顺序,可她们俩争着先出场,最后主持人想出了一个主意,说:“给你们五张卡片,每张卡片上都有一些数.将化简后的数在数轴上表示出来,再用“![]() ”连接起来,(连接化简后的数)谁先按照要求做对,谁先出场”请你帮助她们解决这个问题.
”连接起来,(连接化简后的数)谁先按照要求做对,谁先出场”请你帮助她们解决这个问题.

查看答案和解析>>
科目:初中数学 来源: 题型:
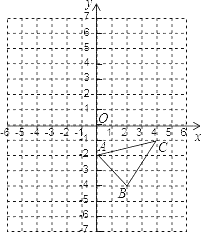
【题目】已知:如图,已知△ABC 中,其中 A(0,﹣2),B(2,﹣4),C(4,﹣1).
(1)画出与△ABC 关于 y 轴对称的图形△A1B1C1;
(2)写出△A1B1C1 各顶点坐标;
(3)求△ABC 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点![]() 、
、![]() 分别为数轴上的两点,点
分别为数轴上的两点,点![]() 对应的数是
对应的数是![]() ,点
,点![]() 对应的数是
对应的数是![]() .现在有一动点
.现在有一动点![]() 从
从![]() 点出发,以每秒
点出发,以每秒![]() 个单位长度的速度向右运动,同时另一动点
个单位长度的速度向右运动,同时另一动点![]() 从点
从点![]() 出发以每秒
出发以每秒![]() 个单位长度的速度向左运动.
个单位长度的速度向左运动.
![]()
(1)与![]() 、
、![]() 两点相等的点
两点相等的点![]() 所对应的数是_________.
所对应的数是_________.
(2)两动点![]() 、
、![]() 相遇时所用时间为________秒;此时两动点所对应的数是_________.
相遇时所用时间为________秒;此时两动点所对应的数是_________.
(3)动点![]() 所对应的数是
所对应的数是![]() 时,此时动点
时,此时动点![]() 所对应的数是_________.
所对应的数是_________.
(4)当动点![]() 运动
运动![]() 秒钟时,动点
秒钟时,动点![]() 与动点
与动点![]() 之的距离是________单位长度.
之的距离是________单位长度.
(5)经过________秒钟,两动点![]() 、
、![]() 在数轴上相距
在数轴上相距![]() 个单位长度.
个单位长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角△ABC 中,∠ACB=90°,AC=BC,D 为 AB 中点,DE⊥DF.
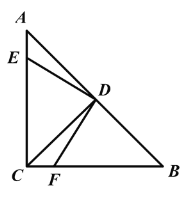
(1)图中有 对全等三角形;
(2)求证:ED=DF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】联想三角形外心的概念,我们可引入如下概念。
定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心。
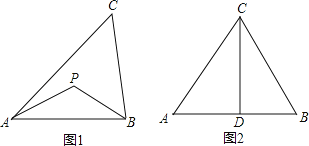
举例:如图1,若PA=PB,则点P为△ABC的准外心。
应用:如图2,CD为等边三角形ABC的高,准外心P在高CD上,且PD=![]() AB,求∠APB的度数。
AB,求∠APB的度数。
探究:已知△ABC为直角三角形,斜边BC=5,AB=3,准外心P在AC边上,试探究PA的长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com