
【题目】把一个等腰直角三角板放在黑板上画好了的平面直角坐标系内,如图,已知直角顶点A的坐标为(0,1),另一个顶点B的坐标为(﹣5,5),则点C的坐标为________.
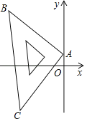
【答案】(﹣4,﹣4)
【解析】
如图,过点B、C分别作BG⊥y轴、CH⊥y轴,先根据AAS证明△ABG≌△CAH,从而可得AG=CH,BG=AH,再根据A、B两点的坐标即可求出OH、CH的长,继而可得点C的坐标.
解:过点B、C分别作BG⊥y轴、CH⊥y轴,垂足分别为G、H,则∠AGB=∠CHA=90°,∠ABG+∠BAG=90°,
∵∠BAC=90°,∴∠CAH+∠BAG=90°,∴∠ABG=∠CAH,
又∵AB=AC,∴△ABG≌△CAH(AAS).
∴AG=CH,BG=AH,
∵A(0,1),∴OA=1,∵B(﹣5,5),∴BG=5,OG=5,
∴AH=5,AG=OG-OA=5-1=4,
∴CH=4,OH=AH-OA=5-1=4,
∴点C的坐标为(―4,―4).
故答案为(―4,―4).



 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:
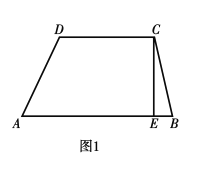
【题目】如图1,梯形![]() 中,上底
中,上底![]() 下底
下底![]() 高
高![]() 梯形的面积
梯形的面积![]() 动点
动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向,以每秒
方向,以每秒![]() 个单位长度的速度匀速运动.
个单位长度的速度匀速运动.
![]() 请根据
请根据![]() 与
与![]() 的关系式,完成下列问题:
的关系式,完成下列问题:
|
|
|
|
| ··· | |
|
|
|
| ··· |
![]() 补充表格中的数据;
补充表格中的数据;
![]() 当
当![]() 时,表示的图形是_ .
时,表示的图形是_ .
![]() 梯形的面积
梯形的面积![]() 与
与![]() 的关系如图2所示,则点
的关系如图2所示,则点![]() 表示的实际意义是_ ;
表示的实际意义是_ ;

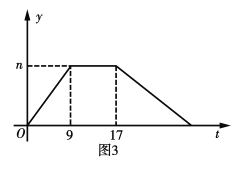
![]() 若点
若点![]() 运动的时间为
运动的时间为![]() 的面积为
的面积为![]() 与
与![]() 的关系如图3所示.求
的关系如图3所示.求![]() 的长和
的长和![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,∠1=∠2,点G为AD的中点,连接BG并延长,交AC于点E,F为AB上一点,且CF⊥AD于点H,下列判断中:①AD是△ABE的角平分线;②BE是△ABD边AD上的中线;③CH是△ACD边AD上的高.正确的个数有( )
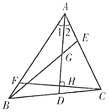
A. 0个B. 1个C. 2个D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC, ∠BAC=90°,D是斜边BC的中点,E,F分别是AB,AC边上的点,且DE⊥DF.
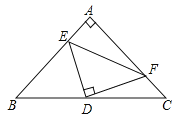
(1)判断DE和DF的数量关系,并说明理由;
(2)若BE=12,CF=5,求△DEF的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算并观察下列各式:
(x1)(x1) ;
(x1)( ![]() x1) ;
x1) ;
(x1)( ![]()
![]() x1) ;
x1) ;
(2)从上面的算式及计算结果,你发现了什么?请根据你发现的规律直接写下面的空格.(x1) ![]() 1;
1;
(3)利用你发现的规律计算:![]() ;
;
(4)利用该规律计算:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的坐标系中,△ABC的三个顶点的坐标依次为A(﹣1,2),B(﹣4,1),C(﹣2,﹣2)
(1)请写出△ABC关于x轴对称的点A1、B1、C1的坐标;
(2)请在这个坐标系中作出△ABC关于y轴对称的△A2B2C2;
(3)计算:△A2B2C2的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
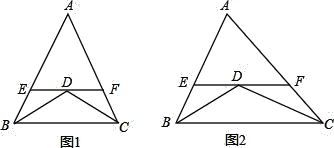
【题目】(1)如图1,已知:在△ABC中,AB=AC=10,BD平分∠ABC,CD平分∠ACB,过点D作EF∥BC,分别交AB、AC于E、F两点,则图中共有__________个等腰三角形;EF与BE、CF之间的数量关系是__________,△AEF的周长是__________;
(2)如图2,若将(1)中“△ABC中,AB=AC=10”该为“若△ABC为不等边三角形,AB=8,AC=10”其余条件不变,则图中共有__________个等腰三角形;EF与BE、CF之间的数量关系是什么?证明你的结论,并求出△AEF的周长;
(3)已知:如图3,D在△ABC外,AB>AC,且BD平分∠ABC,CD平分△ABC的外角∠ACG,过点D作DE∥BC,分别交AB、AC于E、F两点,则EF与BE、CF之间又有何数量关系呢?直接写出结论不证明.
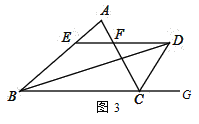
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 地某厂和
地某厂和![]() 地某厂同时制成机器若干台,
地某厂同时制成机器若干台,![]() 地某厂可支援外地
地某厂可支援外地![]() 台,
台,![]() 地某厂可支援外地
地某厂可支援外地![]() 台,现决定给
台,现决定给![]() 地
地![]() 台,
台,![]() 地
地![]() 台,已知从
台,已知从![]() 运往
运往![]() 、
、![]() 两地的运费分别是
两地的运费分别是![]() 元每台、
元每台、![]() 元每台,从
元每台,从![]() 运往
运往![]() 、
、![]() 两地的运费分别是
两地的运费分别是![]() 元每台、
元每台、![]() 元每台.
元每台.
(1)设![]() 地某厂运往
地某厂运往![]() 地
地![]() 台,求总运费为多少元?
台,求总运费为多少元?
(2)在(1)中,当![]() 时,总运费是多少元?
时,总运费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们都知道![]() 表示
表示![]() 与
与![]() 之差的绝对值,实际上也可理解为
之差的绝对值,实际上也可理解为![]() 与
与![]() 两数在数轴上所对的两点之间的距离,试探索:
两数在数轴上所对的两点之间的距离,试探索:
(1)求![]() __________.
__________.
(2)找出所有符合条件的整数![]() ,使得
,使得![]() .满足条件的所有整数值有___________
.满足条件的所有整数值有___________
(3)由以上探索,猜想对于任何有理数![]() ,
,![]() 是否有最大值或最小值?如果有最大值或最小值是多少?
是否有最大值或最小值?如果有最大值或最小值是多少?![]() 有最__________(填“最大”或“最小”)值是__________.
有最__________(填“最大”或“最小”)值是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com