
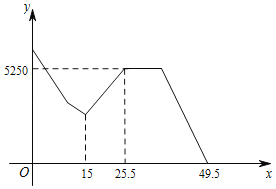
ЁОЬтФПЁПМзЁЂввСНШЫЭЌЪБЦяздааГЕЗжБ№ДгAЁЂBСНЕиГіЗЂЕНABжЎМфЕФCЕиЃЌЧвAЁЂBЁЂCШ§ЕидкЭЌвЛжБЯпЩЯЃЎЕБввЕНДяCЕиЪБМзЛЙЮДЕНДяЃЌввдкCЕиЕШСЫ5ЗжжгЃЌНгЕНМзЕФЕчЛАЫЕЫћЕФздааГЕЛЕСЫашвЊЙЄОпаоРэЃЌгкЪЧввдкCЕиФУСЫЙЄОпЯфСЂМДвддРД![]() БЖЕФЫйЖШЧАЭљМзЛЕГЕДІЃЌввгыМзЛсКЯКѓАяжњМзЛЈСЫ10ЗжжгаоКУздааГЕЃЌШЛКѓСНШЫвдМздРД
БЖЕФЫйЖШЧАЭљМзЛЕГЕДІЃЌввгыМзЛсКЯКѓАяжњМзЛЈСЫ10ЗжжгаоКУздааГЕЃЌШЛКѓСНШЫвдМздРД![]() БЖЕФЫйЖШЦяааЭЌЪБЕНДяCЕиЃЎМзввСНШЫОрCЕиЕФОрРыжЎКЭyЃЈУзЃЉгыМзЫљгУЪБМфxЃЈЗжжгЃЉжЎМфЕФКЏЪ§ЙиЯЕШчЭМЫљЪОЃЈввНгЕчЛАКЭевЙЄОпЯфЕФЪБМфКіТдВЛМЦЃЉЃЌдђAЁЂBСНЕижЎМфЕФОрРыЮЊ___УзЃЎ
БЖЕФЫйЖШЦяааЭЌЪБЕНДяCЕиЃЎМзввСНШЫОрCЕиЕФОрРыжЎКЭyЃЈУзЃЉгыМзЫљгУЪБМфxЃЈЗжжгЃЉжЎМфЕФКЏЪ§ЙиЯЕШчЭМЫљЪОЃЈввНгЕчЛАКЭевЙЄОпЯфЕФЪБМфКіТдВЛМЦЃЉЃЌдђAЁЂBСНЕижЎМфЕФОрРыЮЊ___УзЃЎ
ЁОД№АИЁП6875
ЁОНтЮіЁП
ИљОнЭМЯёЃЌЗжЮіГіУПЖЮКЏЪ§ЭМЯёЫљДњБэЕФЪЕМЪКвхЃЌЭЈЙ§ТЗГЬ=ЫйЖШЁСЪБМфЕФЕШСПЙиЯЕНјааЧѓНтМДПЩ.
ГЕЛЕДІОрCЕиОрРыЃК5250ЁТ2ЃН2625УзЃЌ
ввгУдРД![]() БЖЕФЫйЖШааЪЛетЖЮТЗГЬашвЊЪБМфЮЊЃК25.5-15ЃН10.5ЗжЃЌвђДЫввгУдРД
БЖЕФЫйЖШааЪЛетЖЮТЗГЬашвЊЪБМфЮЊЃК25.5-15ЃН10.5ЗжЃЌвђДЫввгУдРД![]() БЖЕФЫйЖШЮЊЃК2625ЁТ10.5ЃН250Уз/ЗжЃЌввдРДЫйЖШЮЊЃК250ЁТ
БЖЕФЫйЖШЮЊЃК2625ЁТ10.5ЃН250Уз/ЗжЃЌввдРДЫйЖШЮЊЃК250ЁТ![]() ЃН200Уз/ЗжЃЛ
ЃН200Уз/ЗжЃЛ
МзгУдРД![]() БЖЕФЫйЖШааЪЛетЖЮТЗГЬашвЊЪБМфЮЊЃК49.5-25.5-10ЃН14ЗжЃЌвђДЫМзгУдРД
БЖЕФЫйЖШааЪЛетЖЮТЗГЬашвЊЪБМфЮЊЃК49.5-25.5-10ЃН14ЗжЃЌвђДЫМзгУдРД![]() БЖЕФЫйЖШЮЊЃК2625ЁТ14ЃН187.5Уз/ЗжЃЌМздРДЫйЖШЮЊЃК187.5ЁТ
БЖЕФЫйЖШЮЊЃК2625ЁТ14ЃН187.5Уз/ЗжЃЌМздРДЫйЖШЮЊЃК187.5ЁТ![]() ЃН150Уз/ЗжЃЛ
ЃН150Уз/ЗжЃЛ
ЩшвваажСCЕигУЪБxЗжЃЌдђМзаажСГЕЛЕДІЗжЃЌ
гЩЬтвтЕУЃК![]() ЃЌ
ЃЌ
НтЕУЃКxЃН10ЃЌ
ЁрAЁЂBСНЕижЎМфЕФОрРыЮЊЃК![]() УзЃЌ
УзЃЌ
ЙЪД№АИЮЊЃК6875.


 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
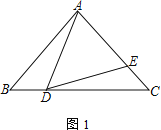
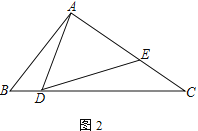
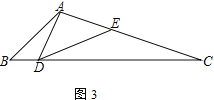
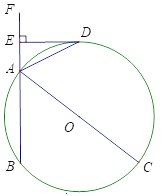
ЁОЬтФПЁПвбжЊЃКЁїABCжаЃЌЕуDЮЊБпBCЩЯвЛЕуЃЌЕуEдкБпACЩЯЃЌЧвЁЯADEЃНЁЯB
(1) ШчЭМ1ЃЌШєABЃНACЃЌЧѓжЄЃК![]() ЃЛ
ЃЛ
(2) ШчЭМ2ЃЌШєADЃНAEЃЌЧѓжЄЃК![]() ЃЛ
ЃЛ
(3) дк(2)ЕФЬѕМўЯТЃЌШєЁЯDACЃН90ЁуЃЌЧвCEЃН4ЃЌtanЁЯBADЃН![]() ЃЌдђABЃН____________ЃЎ
ЃЌдђABЃН____________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ![]() ЪЧ
ЪЧ![]() ЕФЭтНгдВЃЌ
ЕФЭтНгдВЃЌ![]() ЪЧ
ЪЧ![]() ЕФжБОЖЃЌЙ§
ЕФжБОЖЃЌЙ§![]() ЕФжаЕу
ЕФжаЕу![]() зї
зї![]() ЕФжБОЖ
ЕФжБОЖ![]() НЛЯв
НЛЯв![]() гкЕу
гкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() .
.
ЃЈ1ЃЉШчЭМ1ЃЌШєЕу![]() ЪЧЯпЖЮ
ЪЧЯпЖЮ![]() ЕФжаЕуЃЌЧѓ
ЕФжаЕуЃЌЧѓ![]() ЕФЖШЪ§ЃЛ
ЕФЖШЪ§ЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌдк![]() ЩЯШЁвЛЕу
ЩЯШЁвЛЕу![]() ЃЌЪЙ
ЃЌЪЙ![]() ЃЌЧѓжЄЃК
ЃЌЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌШЁ![]() ЕФжаЕу
ЕФжаЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ВЂбгГЄ
ВЂбгГЄ![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() КЭ
КЭ![]() НЛгкЕу
НЛгкЕу![]() ЃЌШє
ЃЌШє![]() ЃЌЧв
ЃЌЧв![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФГЄ.
ЕФГЄ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЙЄГЇФтНЈвЛИіШчЭМЫљЪОЕФОиаЮВжПтABCDЃЌВжПтЕФвЛБпЪЧГЄЮЊ12mЕФвЛУцЧНЃЌСэЭтШ§БпгУ30mГЄЕФНЈжўВФСЯЮЇГЩЃЎЩшABЕФГЄЮЊxmЃЌОиаЮABCIЕФУцЛ§ЮЊSm2ЃЎ
(1)гУКЌxЕФДњЪ§ЪНБэЪОBCЕФГЄЃЌВЂЧѓГіxЕФШЁжЕЗЖЮЇЃЎ
(2)аДГіSЙигкxЕФКЏЪ§ЙиЯЕЪНЃЌВЂЧѓГіSЕФзюДѓжЕЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
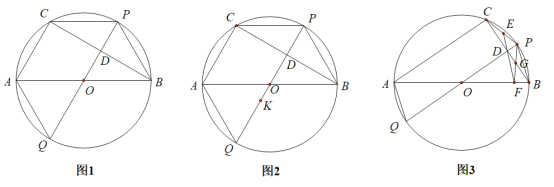
ЁОЬтФПЁПШчЭМЃЌвЛЫвКЃТжЮЛгкЕЦЫўPЕФЖЋББЗНЯђЃЌОрРыЕЦЫў80КЃРяЕФAДІЃЌЫќбие§ФЯЗНЯђКНаавЛЖЮЪБМфКѓЃЌЕНДяЮЛгкЕЦЫўPЕФФЯЦЋЖЋ30ЁуЗНЯђЩЯЕФBДІЃЎ
ЃЈ1ЃЉШєЕЦЫўPжмЮЇ50КЃРяЗЖЮЇФкгаАЕНИЃЌКЃТжДгAДІЕНBДІЕФЭОжаЃЌЪЧЗёгаДЅНИЮЃЯеЃП
ЃЈ2ЃЉШєКЃТжвдУПаЁЪБ30КЃРяЕФЫйЖШДгAДІЕНBДІЃЌЪдХаЖЯКЃТжФмЗёдк5аЁЪБФкЕНДяBДІЃЌВЂЫЕУїРэгЩЃЎЃЈВЮПМЪ§ОнЃК![]() Ёж1.41ЃЌ
Ёж1.41ЃЌ![]() Ёж1.73ЃЌ
Ёж1.73ЃЌ![]() Ёж2.45ЃЉ
Ёж2.45ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
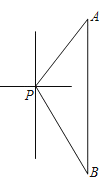
ЁОЬтФПЁПЯЪЗсЫЎЙћЕъМЦЛЎгУ![]() дЊ/КаЕФНјМлЙКНјвЛПюЫЎЙћРёКавдБИЯњЪл.
дЊ/КаЕФНјМлЙКНјвЛПюЫЎЙћРёКавдБИЯњЪл.
![]() ОнЕїВщЃЌЕБИУжжЫЎЙћРёКаЕФЪлМлЮЊ
ОнЕїВщЃЌЕБИУжжЫЎЙћРёКаЕФЪлМлЮЊ![]() дЊ/КаЪБЃЌдТЯњСПЮЊ
дЊ/КаЪБЃЌдТЯњСПЮЊ![]() КаЃЌУПКаЪлМлУПдіГЄ
КаЃЌУПКаЪлМлУПдіГЄ![]() дЊЃЌдТЯњСПОЭЯргІМѕЩй
дЊЃЌдТЯњСПОЭЯргІМѕЩй![]() КаЃЌШєЪЙЫЎЙћРёКаЕФдТЯњСПВЛЕЭгк
КаЃЌШєЪЙЫЎЙћРёКаЕФдТЯњСПВЛЕЭгк![]() КаЃЌУПКаЪлМлгІВЛИпгкЖрЩйдЊ?
КаЃЌУПКаЪлМлгІВЛИпгкЖрЩйдЊ?
![]() дкЪЕМЪЯњЪлЪБЃЌгЩгкЬьЦјКЭдЫЪфЕФдвђЃЌУПКаЫЎЙћРёКаЕФНјМлЬсИпСЫ
дкЪЕМЪЯњЪлЪБЃЌгЩгкЬьЦјКЭдЫЪфЕФдвђЃЌУПКаЫЎЙћРёКаЕФНјМлЬсИпСЫ![]() ЃЌЖјУПКаЫЎЙћРёКаЕФЪлМлБШ(1)жазюИпЪлМлМѕЩйСЫ
ЃЌЖјУПКаЫЎЙћРёКаЕФЪлМлБШ(1)жазюИпЪлМлМѕЩйСЫ![]() ЃЌдТЯњСПБШ(1)жазюЕЭдТЯњСП
ЃЌдТЯњСПБШ(1)жазюЕЭдТЯњСП![]() КадіМгСЫ
КадіМгСЫ![]() ЃЌНсЙћИУдТЫЎЙћЕъЯњЪлИУЫЎЙћРёКаЕФРћШѓДяЕНСЫ
ЃЌНсЙћИУдТЫЎЙћЕъЯњЪлИУЫЎЙћРёКаЕФРћШѓДяЕНСЫ![]() дЊЃЌЧѓ
дЊЃЌЧѓ![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌЯпЖЮ![]() ЪЧЁб
ЪЧЁб![]() ЕФжБОЖЃЌЙ§
ЕФжБОЖЃЌЙ§![]() ЕузїжБЯп
ЕузїжБЯп![]() НЛЁб
НЛЁб![]() гк
гк![]() ЁЂ
ЁЂ![]() СНЕуЃЌЙ§
СНЕуЃЌЙ§![]() Еузї
Еузї![]() ЕФНЧЦНЗжЯпНЛЁб
ЕФНЧЦНЗжЯпНЛЁб![]() гк
гк![]() ЃЌЙ§
ЃЌЙ§![]() зї
зї![]() ЕФДЙЯпНЛ
ЕФДЙЯпНЛ![]() гк
гк![]()
ЃЈ1ЃЉжЄУї![]() ЪЧЁб
ЪЧЁб![]() ЕФЧаЯп
ЕФЧаЯп
ЃЈ2ЃЉжЄУї![]()
ЃЈ3ЃЉШєЁб![]() ЕФжБОЖЮЊ10ЃЌ
ЕФжБОЖЮЊ10ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§ЕФЭМЯѓОЙ§PЃЈ2ЃЌ2ЃЉЃЌЖЅЕуЮЊOЃЈ0ЃЌ0ЃЉЃЌНЋИУЭМЯѓЯђгвЦНвЦЃЌЕБЫќдйДЮОЙ§ЕуPЪБЃЌЫљЕУХзЮяЯпЕФКЏЪ§БэДяЪНЮЊЃЈЁЁЁЁЃЉ
A.yЃН![]() x2B.yЃН
x2B.yЃН![]() ЃЈxЉ2ЃЉ2C.yЃН
ЃЈxЉ2ЃЉ2C.yЃН![]() ЃЈxЉ4ЃЉ2D.yЃН
ЃЈxЉ4ЃЉ2D.yЃН![]() ЃЈxЉ2ЃЉ2+2
ЃЈxЉ2ЃЉ2+2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєвЛЬѕЛЁОЙ§вЛИіЖрБпаЮЯрСкСНБпжаЕуЃЌВЂЧвИУЛЁЩЯЫљгаЕуЖМдкИУЖрБпаЮЕФФкВПЛђБпЩЯЃЌдђГЦИУЛЁЮЊДЫСНБпжаЕуСЌЯпЕФEVAЛЁЃЎР§ШчЃЌЭМ1жаЃЌдкЁїABCжаЃЌDЃЌEЗжБ№ЪЧЁїABCСНБпЕФжаЕуЃЌШчЙћ![]() ЩЯЕФЫљгаЕуЖМдкЁїABCЕФФкВПЛђБпЩЯЃЌдђГЦ
ЩЯЕФЫљгаЕуЖМдкЁїABCЕФФкВПЛђБпЩЯЃЌдђГЦ![]() ЮЊDEЕФвЛЬѕEVAЛЁЃЎ
ЮЊDEЕФвЛЬѕEVAЛЁЃЎ
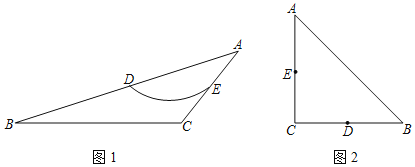
ЃЈ1ЃЉШчЭМ2ЃЌдкRtЁїABCжаЃЌЁЯCЃН90ЁуЃЌACЃНBCЃН4![]() ЃЌDЃЌEЗжБ№ЪЧBCЃЌACЕФжаЕуЃЌЛГіDEЕФзюГЄЕФEVAЛЁ
ЃЌDЃЌEЗжБ№ЪЧBCЃЌACЕФжаЕуЃЌЛГіDEЕФзюГЄЕФEVAЛЁ![]() ЃЌВЂжБНгаДГіДЫЪБ
ЃЌВЂжБНгаДГіДЫЪБ![]() ЕФГЄЃЛ
ЕФГЄЃЛ
ЃЈ2ЃЉдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊЕуAЃЈ0ЃЌ4ЃЉЃЌBЃЈ0ЃЌ0ЃЉЃЌCЃЈ4tЃЌ0ЃЉЃЈtЃО0ЃЉЃЌдкЁїABCжаЃЌDЃЌEЗжБ№ЪЧABЃЌACЕФжаЕуЃЎ
ЂйШєtЃН1ЃЌЧѓDEЕФEVAЛЁ![]() ЫљдкдВЕФдВаФPЕФзнзјБъmЕФШЁжЕЗЖЮЇЃЛ
ЫљдкдВЕФдВаФPЕФзнзјБъmЕФШЁжЕЗЖЮЇЃЛ
ЂкШєдкЁїABCжаДцдквЛЬѕDEЕФEVAЛЁ![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЫљдкдВЕФдВаФPдкЁїABCЕФФкВПЛђБпЩЯЃЌжБНгаДГіtЕФШЁжЕЗЖЮЇЃЎ
ЫљдкдВЕФдВаФPдкЁїABCЕФФкВПЛђБпЩЯЃЌжБНгаДГіtЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com