
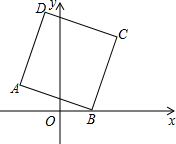
 如图,在平面直角坐标系xOy中,点B是x轴上一动点,且点A(-3,2),连接AB,以AB为边向上作正方形ABCD.
如图,在平面直角坐标系xOy中,点B是x轴上一动点,且点A(-3,2),连接AB,以AB为边向上作正方形ABCD.
|

| (-x+3)2+(-x-1-2)2 |
| 2x2+18 |
| 18 |
| 2 |


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
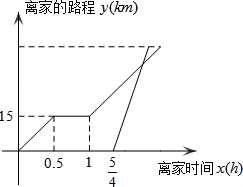 周末,小明骑电动车从家里出发到野外郊游.从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地.小明离家1小时15分钟后,妈妈驾车沿相同路线前往乙地,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.已知妈妈驾车的速度是小明骑车速度的2倍.
周末,小明骑电动车从家里出发到野外郊游.从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地.小明离家1小时15分钟后,妈妈驾车沿相同路线前往乙地,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.已知妈妈驾车的速度是小明骑车速度的2倍.查看答案和解析>>
科目:初中数学 来源: 题型:
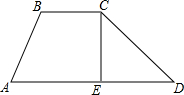 如图,水库大坝的横断面近似于梯形ABCD,迎水坡BC的倾斜角∠D=30°,背水坡AB的坡比为1.2:1,坝顶BC=6米,坝高CE=8米,求CD和AD的长.
如图,水库大坝的横断面近似于梯形ABCD,迎水坡BC的倾斜角∠D=30°,背水坡AB的坡比为1.2:1,坝顶BC=6米,坝高CE=8米,求CD和AD的长.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com