
°æƒø°ø∂‘”⁄∆Ω√Ê÷±Ω«◊¯±ÍœµxOy÷–µƒµ„P∫ÕÕº–ŒG£¨∏¯≥ˆ»Áœ¬∂®“£∫Ω´µ„P—ÿœÚ”“ªÚœÚ…œµƒ∑ΩœÚ∆Ω“∆“ª¥Œ£¨∆Ω“∆æý¿ÎŒ™d£®d£æ0£©∏ˆ≥§∂»µ•Œª£¨∆Ω“∆∫Ûµƒµ„º«Œ™P°‰£¨»Ùµ„P°‰‘⁄Õº–ŒG…œ£¨‘Ú≥∆µ„PŒ™Õº–ŒGµƒ°∞¥Ô≥…µ„°±£ÆÃÿ±µÿ£¨µ±µ„P‘⁄Õº–ŒG…œ ±£¨µ„P «Õº–ŒGµƒ°∞¥Ô≥…µ„°±£Æ¿˝»Á£¨µ„P£®©Å1£¨0£© «÷±œþy£Ωxµƒ°∞¥Ô≥…µ„°±£Æ
“—÷™°—Oµƒ∞Îæ∂Œ™1£¨÷±œþl£∫y£Ω©Åx+b£Æ
£®1£©µ±b£Ω©Å3 ±£¨
¢Ÿ‘⁄O£®0£¨0£©£¨A£®©Å4£¨1£©£¨B£®©Å4£¨©Å1£©»˝µ„÷–£¨ «÷±œþlµƒ°∞¥Ô≥…µ„°±µƒ «£∫_____£ª
¢⁄»Ù÷±œþl…œµƒµ„M£®m£¨n£© «°—Oµƒ°∞¥Ô≥…µ„°±£¨«Ûmµƒ»°÷µ∑∂Œß£ª
£®2£©µ„P‘⁄÷±œþl…œ£¨«“µ„P «°—Oµƒ°∞¥Ô≥…µ„°±£Æ»ÙÀ˘”–¬˙◊„Ãıº˛µƒµ„Pππ≥…“ªÃı≥§∂»≤ªŒ™0µƒœþ∂Œ£¨«Î÷±Ω”–¥≥ˆbµƒ»°÷µ∑∂Œß£Æ

°æ¥∞∏°ø£®1£©¢ŸA£¨B£ª¢⁄©Å4°Ðm°Ð©Å2ªÚ©Å1°Ðm°Ð1£ª£®2£©©Å2°Ðb£º![]() £Æ
£Æ
°æΩ‚Œˆ°ø
£®1£©¢Ÿ∏˘æð°∞¥Ô≥…µ„°±µƒ∂®“º¥ø…Ω‚æˆŒ £Æ
¢⁄π˝µ„£®0£¨1£©∫Õµ„£®0£¨©Å1£©◊˜x÷·µƒ∆Ω––œþ∑÷±Ωª÷±œþl”⁄M1£¨M2£¨π˝µ„£®1£¨0£©∫Õµ„£®©Å1£¨0£©◊˜y÷·µƒ∆Ω––œþ∑÷±Ωª÷±œþl”⁄M3£¨M4£¨”…¥Àº¥ø…≈–∂œ£Æ
£®2£©µ±M2”ÎM3÷ÿ∫œ£¨◊¯±ÍŒ™£®©Å1£¨©Å1£© ±£¨©Å1£Ω1+b£¨ø…µ√b£Ω©Å2£ªµ±÷±œþl”ΰ—Oœý«– ±£¨…Ë«–µ„Œ™E£¨Ωªy÷·”⁄F£¨«Û≥ˆµ„Eµƒ◊¯±Í£¨º¥ø…≈–∂œ£Æ
£®1£©¢Ÿ°þb£Ω©Å3 ±£¨÷±œþl£∫y£Ω©Åx©Å3£¨
°ý÷±œþl”Îx÷·µƒΩªµ„Œ™£∫£®©Å3£¨0£©£¨÷±œþl”Îy÷·µƒΩªµ„Œ™£∫£®0£¨©Å3£©£¨
°ýO£®0£¨0£©‘⁄÷±œþlµƒ…œ∑Ω£¨
°ýO£®0£¨0£©≤ª «÷±œþlµƒ°∞¥Ô≥…µ„°±£¨
°þµ±x£Ω©Å4 ±£¨y£Ω4©Å3£Ω1£¨
°ýµ„A£®©Å4£¨1£©‘⁄÷±œþl…œ£¨
°ýµ„A «÷±œþlµƒ°∞¥Ô≥…µ„°±£¨
°þµ„B£®©Å4£¨©Å1£©‘⁄÷±œþlµƒœ¬∑Ω£¨∞—µ„B£®©Å4£¨©Å1£©œÚ…œ∆Ω“∆2∏ˆ≥§∂»µ•ŒªŒ™£®©Å4£¨1£©£¨
°ýµ„B «÷±œþlµƒ°∞¥Ô≥…µ„°±£¨
π ¥∞∏Œ™£∫A£¨B£ª
¢⁄…Ë÷±œþl£∫y£Ω©Åx©Å3£¨∑÷±”Î÷±œþy£Ω1°¢y£Ω©Å1°¢x£Ω©Å1°¢x£Ω1“¿¥ŒΩª”⁄µ„M1°¢M2°¢M3°¢M4£¨»ÁÕº1À˘ æ£∫
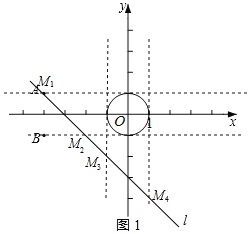
‘Úµ„M1£¨M2£¨M3£¨M4µƒ∫·◊¯±Í∑÷±Œ™©Å4°¢©Å2°¢©Å1°¢1£¨
œþ∂ŒM1M2…œµƒµ„œÚ”“µƒ∑ΩœÚ∆Ω“∆”ΰ—OƒÐœýΩª£¨œþ∂ŒM3M4…œµƒµ„œÚ…œµƒ∑ΩœÚ∆Ω“∆”ΰ—OƒÐœýΩª£¨
°ýœþ∂ŒM1M2∫Õœþ∂ŒM3M4…œµƒµ„ «°—Oµƒ°∞¥Ô≥…µ„°±£¨
°ýmµƒ»°÷µ∑∂Œß «©Å4°Ðm°Ð©Å2ªÚ©Å1°Ðm°Ð1£ª
£®2£©»ÁÕº2À˘ æ£∫
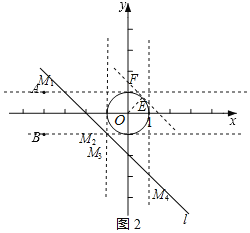
µ±M2”ÎM3÷ÿ∫œ£¨◊¯±ÍŒ™£®©Å1£¨©Å1£© ±£¨©Å1£Ω1+b£¨°ýb£Ω©Å2£ª
¢⁄µ±÷±œþl”ΰ—Oœý«– ±£¨…Ë«–µ„Œ™E£¨Ωªy÷·”⁄F£Æ
”…“‚£¨‘⁄Rt°˜OEF÷–£¨°œOEF£Ω90°„£¨OE£Ω1£¨°œEOF£Ω45°„£¨
°ý°˜OEF «µ»—¸÷±Ω«»˝Ω«–Œ£¨
°ýOF£Ω![]() OE£Ω
OE£Ω![]() £ª
£ª
π€≤ÏÕºœÛø…÷™¬˙◊„Ãıº˛µƒbµƒ÷µŒ™©Å2°Ðb£º![]() £Æ
£Æ



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™£∫»ÁÕº¢Ÿ£¨‘⁄æÿ–ŒABCD÷–£¨AB=5£¨AD=![]() £¨AE°ÕBD£¨¥π◊„ «E£¨µ„F «µ„Eπÿ”⁄ABµƒ∂‘≥∆µ„£¨¡¨Ω”AF°¢BF
£¨AE°ÕBD£¨¥π◊„ «E£¨µ„F «µ„Eπÿ”⁄ABµƒ∂‘≥∆µ„£¨¡¨Ω”AF°¢BF
£®1£©«ÛAE∫ÕBEµƒ≥§£ª
£®2£©»ÙΩ´°˜ABF—ÿ◊≈…‰œþBD∑ΩœÚ∆Ω“∆£¨…Ë∆Ω“∆µƒæý¿ÎŒ™m£®∆Ω“∆æý¿Î÷∏µ„B—ÿBD∑ΩœÚÀ˘æ≠π˝µƒœþ∂Œ≥§∂»£©.µ±µ„F∑÷±∆Ω“∆µΩœþ∂ŒAB°¢AD…œ ±£¨÷±Ω”–¥≥ˆœý”¶µƒmµƒ÷µ£ª
£®3£©»ÁÕº¢⁄£¨Ω´°˜ABF»∆µ„BÀ≥ ±’Ζ˝◊™“ª∏ˆΩ«¶¡£®0°„£º¶¡£º180°„£©£¨º«–˝◊™÷–µƒ°˜ABFŒ™°˜A°‰BF°‰£¨‘⁄–˝◊™π˝≥Ã÷–£¨…ËA°‰F°‰À˘‘⁄µƒ÷±œþ”Î÷±œþADΩª”⁄µ„P£¨”Î÷±œþBDΩª”⁄µ„Q. «∑ҥʑ⁄’‚—˘µƒP°¢Q¡Ωµ„£¨ π°˜DPQŒ™µ»—¸»˝Ω«–Œ£ø»Ù¥Ê‘⁄£¨«Û≥ˆ¥À ±DQµƒ≥§£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨≈◊ŒÔœþy£Ωax2+2x+cæ≠π˝µ„A£®0£¨3£©£¨B£®©Å1£¨0£©£¨«ÎΩ‚¥œ¬¡–Œ £∫
£®1£©«Û≈◊ŒÔœþµƒΩ‚Œˆ Ω£ª
£®2£©≈◊ŒÔœþµƒ∂•µ„Œ™µ„D£¨∂‘≥∆÷·”Îx÷·Ωª”⁄µ„E£¨¡¨Ω”BD£¨«ÛBDµƒ≥§£ª
£®3£©µ„F‘⁄≈◊ŒÔœþ…œ‘À∂Ø£¨ «∑ҥʑ⁄µ„F£¨ π°˜BFCµƒ√ʪ˝Œ™6£¨»Áπ˚¥Ê‘⁄£¨«Û≥ˆµ„Fµƒ◊¯±Í£ª»Áπ˚≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø£®“—÷™£∫»ÁÕºÀ˘ 浃“ª’≈æÿ–Œ÷Ω∆¨ABCD£®AD>AB£©£¨Ω´÷Ω∆¨’€µ˛“ª¥Œ£¨ πµ„A”ε„C÷ÿ∫œ£¨‘Ÿ’πø™£¨’€∫€EFΩªAD±þ”⁄µ„E£¨ΩªBC±þ”⁄µ„F£¨∑÷±¡¨Ω·AF∫ÕCE£Æ
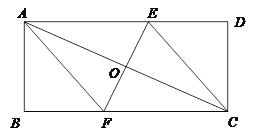
£®1£©«Û÷§£∫Àƒ±þ–ŒAFCE «¡‚–Œ£ª
£®2£©»ÙAE=10cm£¨°˜ABFµƒ√ʪ˝Œ™24cm2£¨«Û°˜ABFµƒ÷Ð≥§£ª
£®3£©‘⁄œþ∂ŒAC…œ «∑ҥʑ⁄“ªµ„P£¨ πµ√2AE2=AC°§AP£ø»Ù¥Ê‘⁄£¨«ÎÀµ√˜µ„PµƒŒª÷√£¨≤¢”Ë“‘÷§√˜£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
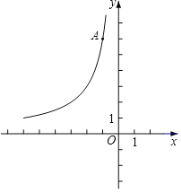
°æƒø°ø»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±ÍœµxOy÷–£¨∫Ø ˝y£Ω![]() £®x£º0£©µƒÕºœÛæ≠π˝µ„A£®©Å1£¨6£©£Æ
£®x£º0£©µƒÕºœÛæ≠π˝µ„A£®©Å1£¨6£©£Æ
£®1£©«Ûkµƒ÷µ£ª
£®2£©“—÷™µ„P£®a£¨©Å2a£©£®a£º0£©£¨π˝µ„P◊˜∆Ω––”⁄x÷·µƒ÷±œþ£¨Ωª÷±œþy£Ω©Å2x©Å2”⁄µ„M£¨Ωª∫Ø ˝y£Ω![]() £®x£º0£©µƒÕºœÛ”⁄µ„N£Æ
£®x£º0£©µƒÕºœÛ”⁄µ„N£Æ
¢Ÿµ±a£Ω©Å1 ±£¨«Ûœþ∂ŒPM∫ÕPNµƒ≥§£ª
¢⁄»ÙPN°ð2PM£¨Ω·∫œ∫Ø ˝µƒÕºœÛ£¨÷±Ω”–¥≥ˆaµƒ»°÷µ∑∂Œß£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨≈◊ŒÔœþ![]() ”Î
”Î![]() ÷·Ωª”⁄µ„
÷·Ωª”⁄µ„![]() ∫Õ
∫Õ![]() £¨”Î
£¨”Î![]() ÷·Ωª”⁄µ„
÷·Ωª”⁄µ„![]() ∂•µ„Œ™
∂•µ„Œ™![]() £Æ
£Æ
![]() «Û≈◊ŒÔœþµƒΩ‚Œˆ Ω£ª
«Û≈◊ŒÔœþµƒΩ‚Œˆ Ω£ª
![]() «Û
«Û![]() µƒ∂» ˝£ª
µƒ∂» ˝£ª
![]() »Ùµ„
»Ùµ„![]() «œþ∂Œ
«œþ∂Œ![]() …œ“ª∏ˆ∂ص„£¨π˝
…œ“ª∏ˆ∂ص„£¨π˝![]() ◊˜
◊˜![]() ÷·Ωª≈◊ŒÔœþ”⁄µ„
÷·Ωª≈◊ŒÔœþ”⁄µ„![]() £¨Ωª
£¨Ωª![]() ÷·”⁄µ„
÷·”⁄µ„![]() £¨…Ë
£¨…Ë![]() µ„µƒ∫·◊¯±ÍŒ™
µ„µƒ∫·◊¯±ÍŒ™![]() £Æ
£Æ
¢Ÿ«Ûœþ∂Œ![]() µƒ◊Ó¥Û÷µ£ª
µƒ◊Ó¥Û÷µ£ª
¢⁄»Ù![]() «µ»—¸»˝Ω«–Œ£¨÷±Ω”–¥≥ˆ
«µ»—¸»˝Ω«–Œ£¨÷±Ω”–¥≥ˆ![]() µƒ÷µ£Æ
µƒ÷µ£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
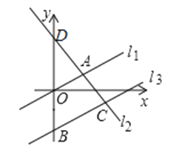
°æƒø°ø»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨÷±œþ![]() ”Î÷±œþ
”Î÷±œþ![]() £¨Ωªµ„
£¨Ωªµ„![]() µƒ∫·◊¯±ÍŒ™
µƒ∫·◊¯±ÍŒ™![]() £¨Ω´÷±œþ
£¨Ω´÷±œþ![]() £¨—ÿ
£¨—ÿ![]() ÷·œÚœ¬∆Ω“∆
÷·œÚœ¬∆Ω“∆![]() ∏ˆµ•Œª≥§∂»£¨µ√µΩ÷±œþ
∏ˆµ•Œª≥§∂»£¨µ√µΩ÷±œþ![]() £¨÷±œþ
£¨÷±œþ![]() £¨”Î
£¨”Î![]() ÷·Ωª”⁄µ„
÷·Ωª”⁄µ„![]() £¨”Î÷±œþ
£¨”Î÷±œþ![]() £¨Ωª”⁄µ„
£¨Ωª”⁄µ„![]() £¨µ„
£¨µ„![]() µƒ◊ð◊¯±ÍŒ™
µƒ◊ð◊¯±ÍŒ™![]() £¨÷±œþ
£¨÷±œþ![]() £ª”Î
£ª”Î![]() ÷·Ωª”⁄µ„
÷·Ωª”⁄µ„![]() £Æ
£Æ
£®1£©«Û÷±œþ![]() µƒΩ‚Œˆ Ω£ª
µƒΩ‚Œˆ Ω£ª
£®2£©«Û![]() µƒ√ʪ˝
µƒ√ʪ˝
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥…õÍ≥ˆ €“ªøÓ…Ã∆∑£¨æ≠ –≥°µ˜≤È∑¥”≥£¨∏√…Ã∆∑µƒ»’œ˙ €¡øy£®º˛£©”Îœ˙ €µ•º€x£®‘™£©÷ƺ‰¬˙◊„“ª¥Œ∫Ø ˝πÿœµ£¨πÿ”⁄∏√…Ã∆∑µƒœ˙ €µ•º€£¨»’œ˙ €¡ø£¨»’œ˙ €¿˚»Ûµƒ≤ø∑÷∂‘”¶ ˝æð»Á±Ì£∫[◊¢£∫»’œ˙ €¿˚»Û£Ω»’œ˙ €¡ø°¡£®œ˙ €µ•º€©Å≥…±æµ•º€£©
œ˙ €µ•º€x£®‘™£© | 75 | 78 | 82 |
»’œ˙ €¡øy£®º˛£© | 150 | 120 | 80 |
»’œ˙ €¿˚»Ûw£®‘™£© | 5250 | a | 3360 |
£®1£©∏˘æð“‘…œ–≈œ¢£¨ÃÓø’£∫∏√≤˙∆∑µƒ≥…±æµ•º€ «°° °°‘™£¨±Ì÷–aµƒ÷µ «°° °°£¨yπÿ”⁄xµƒ∫Ø ˝πÿœµ Ω «°° °°£ª
£®2£©«Û∏√…Ã∆∑»’œ˙ €¿˚»Ûµƒ◊Ó¥Û÷µ£Æ
£®3£©”…”⁄ƒ≥÷÷‘≠“Ú£¨∏√…Ã∆∑Ω¯º€ΩµµÕ¡Àm‘™/º˛£®m£æ0£©£¨∏√…õ͑⁄ΩÒ∫Ûµƒœ˙ €÷–£¨…õÍπÊ∂®∏√…Ã∆∑µƒœ˙ €µ•º€≤ªµÕ”⁄68‘™£¨»’œ˙ €¡ø”Îœ˙ €µ•º€»‘»ª¬˙◊„£®1£©÷–µƒ∫Ø ˝πÿœµ£¨»Ù»’œ˙ €◊Ó¥Û¿˚»Û «6600‘™£¨÷±Ω”–¥≥ˆmµƒ÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨≈◊ŒÔœþ![]() µƒ∂‘≥∆÷·Œ™÷±œþ
µƒ∂‘≥∆÷·Œ™÷±œþ![]() £¨”Î
£¨”Î![]() ÷·µƒ
÷·µƒ![]() ∏ˆΩªµ„◊¯±ÍŒ™
∏ˆΩªµ„◊¯±ÍŒ™![]() £¨
£¨![]() £¨∆‰≤ø∑÷ÕºœÛ»ÁÕºÀ˘ 棨œ¬¡–Ω·¬€£∫¢Ÿ
£¨∆‰≤ø∑÷ÕºœÛ»ÁÕºÀ˘ 棨œ¬¡–Ω·¬€£∫¢Ÿ![]() £ª¢⁄∑Ω≥Ã
£ª¢⁄∑Ω≥Ã![]() µƒ¡Ω∏ˆ∏˘ «
µƒ¡Ω∏ˆ∏˘ «![]() £¨
£¨![]() £ª¢€
£ª¢€![]() £ª¢Ðµ±
£ª¢Ðµ±![]() ±£¨
±£¨![]() µƒ»°÷µ∑∂Œß «
µƒ»°÷µ∑∂Œß «![]() £Æ∆‰÷–Ω·¬€’˝»∑µƒ∏ˆ ˝ «£® £©
£Æ∆‰÷–Ω·¬€’˝»∑µƒ∏ˆ ˝ «£® £©
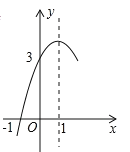
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com