
【题目】(已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连结AF和CE.
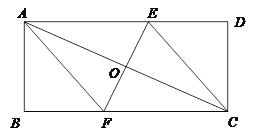
(1)求证:四边形AFCE是菱形;
(2)若AE=10cm,△ABF的面积为24cm2,求△ABF的周长;
(3)在线段AC上是否存在一点P,使得2AE2=AC·AP?若存在,请说明点P的位置,并予以证明;若不存在,请说明理由.
【答案】(1)证明见解析;(2)24cm;(3)存在,过E作EP⊥AD交AC于P,则P就是所求的点,证明见解析.
【解析】
(1)由四边形ABCD是矩形与折叠的性质,易证得△AOE≌△COF,即可得AE=CF,则可证得四边形AFCE是平行四边形,又由AC⊥EF,则可证得四边形AFCE是菱形;
(2)由已知可得:S△ABF=![]() ABBF=24cm2,则可得AB2+BF2=(AB+BF)2-2ABBF=(AB+BF)2-2×48=AF2=100(cm2),则可求得AB+BF的值,继而求得△ABF的周长.
ABBF=24cm2,则可得AB2+BF2=(AB+BF)2-2ABBF=(AB+BF)2-2×48=AF2=100(cm2),则可求得AB+BF的值,继而求得△ABF的周长.
(3)过E作EP⊥AD交AC于P,则P就是所求的点,首先证明四边形AFCE是菱形,然后根据题干条件证明△AOE∽△AEP,列出关系式.
解:(1)∵四边形ABCD是矩形,
∴AD∥BC,∴∠EAO=∠FCO,
由折叠的性质可得:OA=OC,AC⊥EF,
在△AOE和△COF中,
∵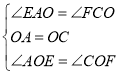 ,
,
∴△AOE≌△COF(ASA),
∴AE=CF,
∴四边形AFCE是平行四边形,
∵AC⊥EF,
∴四边形AFCE是菱形;
(2)∵四边形AFCE是菱形,
∴AF=AE=10cm,
∵四边形ABCD是矩形,
∴∠B=90°,
∴S△ABF=![]() ABBF=24cm2,
ABBF=24cm2,
∴ABBF=48(cm2),
∴AB2+BF2=(AB+BF)2-2ABBF=(AB+BF)2-2×48=AF2=100(cm2),
∴AB+BF=14(cm)
∴△ABF的周长为:AB+BF+AF=14+10=24(cm).
(3)证明:过E作EP⊥AD交AC于P,则P就是所求的点.
当顶点A与C重合时,折痕EF垂直平分AC,
∴OA=OC,∠AOE=∠COF=90°,
∵在平行四边形ABCD中,AD∥BC,
∴∠EAO=∠FCO,
∴△AOE≌△COF,
∴OE=OF
∴四边形AFCE是菱形.
∴∠AOE=90°,又∠EAO=∠EAP,
由作法得∠AEP=90°,
∴△AOE∽△AEP,
∴![]() ,则AE2=AOAP,
,则AE2=AOAP,
∵四边形AFCE是菱形,
∴AO=![]() AC,
AC,
∴AE2=![]() ACAP,
ACAP,
∴2AE2=ACAP.


科目:初中数学 来源: 题型:
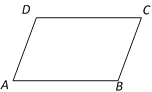
【题目】已知:在平行四边形ABCD中,AB︰BC=3︰2.
(1)根据条件画图:作∠BCD的平分线,交边AB于点E,取线段BE的中点F,连接DF交CE于点G.
(2)设![]() ,那么向量
,那么向量![]() =______.(用向量
=______.(用向量![]() 、
、![]() 表示),并在图中画出向量
表示),并在图中画出向量![]() 在向量
在向量![]() 和
和![]() 方向上的分向量.
方向上的分向量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD 中,对角线AC,BD交于点O,以 AD,OD为邻边作平行四边形ADOE,连接BE.
(1) 求证:四边形AOBE是菱形;
(2) 若∠EAO+∠DCO=180°,DC=2,求四边形ADOE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图有两个边长为4cm的正方形,其中一个正方形的顶点在另一个正方形的中心上,那么图中阴影部分的面积是( )
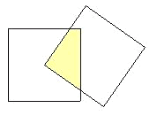
A.4cm2B.8cm2
C.16cm2D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
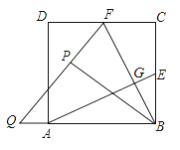
【题目】如图,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE,BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交BA延长线于点Q,下列结论正确的个数是( )
①AE=BF;②AE⊥BF;③sin∠BQP=![]() ;④S四边形ECFG=2S△BGE.
;④S四边形ECFG=2S△BGE.
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年第六届世界互联网大会在乌镇召开,小南和小西参加了某分会场的志愿服务工作,本次志愿服务工作一共设置了三个岗位,分别是引导员、联络员和咨询员.请你用画树状图或列表法求出小南和小西恰好被分配到同一个岗位进行志愿服务的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P和图形G,给出如下定义:将点P沿向右或向上的方向平移一次,平移距离为d(d>0)个长度单位,平移后的点记为P′,若点P′在图形G上,则称点P为图形G的“达成点”.特别地,当点P在图形G上时,点P是图形G的“达成点”.例如,点P(﹣1,0)是直线y=x的“达成点”.
已知⊙O的半径为1,直线l:y=﹣x+b.
(1)当b=﹣3时,
①在O(0,0),A(﹣4,1),B(﹣4,﹣1)三点中,是直线l的“达成点”的是:_____;
②若直线l上的点M(m,n)是⊙O的“达成点”,求m的取值范围;
(2)点P在直线l上,且点P是⊙O的“达成点”.若所有满足条件的点P构成一条长度不为0的线段,请直接写出b的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级一班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”“戏剧”“散文”“其他”四个类型,每位同学仅选一项,根据调查结果绘制了不完整的频数分布表和扇形统计图.
类别 | 频数(人数) | 频率 |
小说 | 0.5 | |
戏剧 | 4 | |
散文 | 10 | 0.25 |
其他 | 6 | |
合计 | 1 |
根据图表提供的信息,解答下列问题:
(1)八年级一班有多少名学生?
(2)请补全频数分布表,并求出扇形统计图中“其他”类所占的百分比;
(3)在调查问卷中,甲、乙、丙、丁四位同学选择了“戏剧”类,现从以上四位同学中任意选出2名同学参加学校的戏剧兴趣小组,请用画树状图或列表法的方法,求选取的2人恰好是乙和丙的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游乐园有一个直径为16米的圆形喷水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物线,在距水池中心3米处达到最高,高度为5米,且各方向喷出的水柱恰好在喷水池中心的装饰物处回合,如图所示,以水平方向为![]() 轴,喷水池中心为原点建立平面直角坐标系.
轴,喷水池中心为原点建立平面直角坐标系.
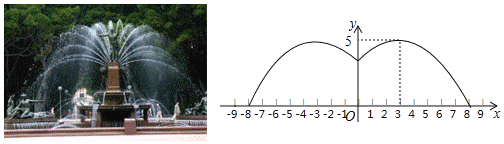
(1)求水柱所在抛物线(第一象限部分)的函数表达式;
(2)王师傅在喷水池内维修设备期间,喷水管意外喷水,为了不被淋湿,身高1.8米的王师傅站立时必须在离水池中心多少米以内?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com