
【题目】如图,抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,与
,与![]() 轴的
轴的![]() 个交点坐标为
个交点坐标为![]() ,
,![]() ,其部分图象如图所示,下列结论:①
,其部分图象如图所示,下列结论:①![]() ;②方程
;②方程![]() 的两个根是
的两个根是![]() ,
,![]() ;③
;③![]() ;④当
;④当![]() 时,
时,![]() 的取值范围是
的取值范围是![]() .其中结论正确的个数是( )
.其中结论正确的个数是( )
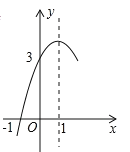
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P和图形G,给出如下定义:将点P沿向右或向上的方向平移一次,平移距离为d(d>0)个长度单位,平移后的点记为P′,若点P′在图形G上,则称点P为图形G的“达成点”.特别地,当点P在图形G上时,点P是图形G的“达成点”.例如,点P(﹣1,0)是直线y=x的“达成点”.
已知⊙O的半径为1,直线l:y=﹣x+b.
(1)当b=﹣3时,
①在O(0,0),A(﹣4,1),B(﹣4,﹣1)三点中,是直线l的“达成点”的是:_____;
②若直线l上的点M(m,n)是⊙O的“达成点”,求m的取值范围;
(2)点P在直线l上,且点P是⊙O的“达成点”.若所有满足条件的点P构成一条长度不为0的线段,请直接写出b的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】Rt△ABC中,∠ABC=90°,AB=3,BC=4,过点B的直线把△ABC分割成两个三角形,使其中只有一个是等腰三角形,则这个等腰三角形的面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游乐园有一个直径为16米的圆形喷水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物线,在距水池中心3米处达到最高,高度为5米,且各方向喷出的水柱恰好在喷水池中心的装饰物处回合,如图所示,以水平方向为![]() 轴,喷水池中心为原点建立平面直角坐标系.
轴,喷水池中心为原点建立平面直角坐标系.
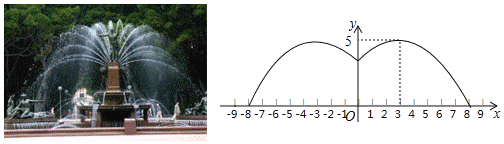
(1)求水柱所在抛物线(第一象限部分)的函数表达式;
(2)王师傅在喷水池内维修设备期间,喷水管意外喷水,为了不被淋湿,身高1.8米的王师傅站立时必须在离水池中心多少米以内?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种商品的标价为![]() 元/件,经过两次降价后的价格为
元/件,经过两次降价后的价格为![]() 元/件,并且两次降价的百分率相同.
元/件,并且两次降价的百分率相同.
(1)求该种商品每次降价的百分率;
(2)若该种商品进价为![]() 元/件,两次降价共售出此种商品
元/件,两次降价共售出此种商品![]() 件,为使两次降价销售的总利润不少于
件,为使两次降价销售的总利润不少于![]() 元,则第一次降价后至少要售出该种商品多少件?
元,则第一次降价后至少要售出该种商品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示为两把按不同比例尺进行刻度的直尺,每把直尺的刻度都是均匀的,已知两把直尺在刻度10处是对齐的,且上面的直尺在刻度15处与下面的直尺在刻度18处也刚好对齐,则上面直尺的刻度16与下面直尺对应的刻度是( )
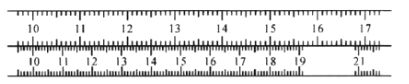
A.19.4B.19.5C.19.6D.19.7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】锐角![]() 中,
中,![]() ,
,![]() 为
为![]() 边上的高线,
边上的高线,![]() ,两动点
,两动点![]() 分别在边
分别在边![]() 上滑动,且
上滑动,且![]() ,以
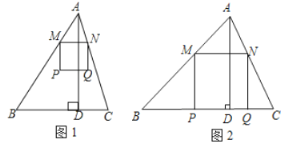
,以![]() 为边向下作正方形
为边向下作正方形![]() (如图1),设其边长为
(如图1),设其边长为![]() .
.
(1)当![]() 恰好落在边
恰好落在边![]() 上(如图2)时,求
上(如图2)时,求![]() ;
;
(2)正方形![]() 与
与![]() 公共部分的面积为
公共部分的面积为![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
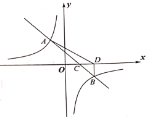
【题目】一次函数![]() 的图像与双曲线
的图像与双曲线![]()
![]() 相交于
相交于![]() 和
和![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() ,过点
,过点![]() 作
作![]() 轴,垂足为点
轴,垂足为点![]() .
.
(1)求一次函数的解析式;
(2)根据图像直接写出不等式![]() 的解集;
的解集;
(3)![]() 的面积为
的面积为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某玩具厂生产一种玩具,本着控制固定成本,降价促销的原则,使生产的玩具能够全部售出.据市场调查,若按每个玩具280元销售时,每月可销售300个.若销售单价每降低1元,每月可多售出2个.据统计,每个玩具的固定成本Q(元)与月产销量y(个)满足如下关系:
月产销量y(个) | … | 160 | 200 | 240 | 300 | … |
每个玩具的固定成本Q(元) | … | 60 | 48 | 40 | 32 | … |
(1)写出月产销量y(个)与销售单价x (元)之间的函数关系式;
(2)求每个玩具的固定成本Q(元)与月产销量y(个)之间的函数关系式;
(3)若每个玩具的固定成本为30元,则它占销售单价的几分之几?
(4)若该厂这种玩具的月产销量不超过400个,则每个玩具的固定成本至少为多少元?销售单价最低为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com