
【题目】某种商品的标价为![]() 元/件,经过两次降价后的价格为
元/件,经过两次降价后的价格为![]() 元/件,并且两次降价的百分率相同.
元/件,并且两次降价的百分率相同.
(1)求该种商品每次降价的百分率;
(2)若该种商品进价为![]() 元/件,两次降价共售出此种商品
元/件,两次降价共售出此种商品![]() 件,为使两次降价销售的总利润不少于
件,为使两次降价销售的总利润不少于![]() 元,则第一次降价后至少要售出该种商品多少件?
元,则第一次降价后至少要售出该种商品多少件?
【答案】(1) 10%;(2)23件.
【解析】
(1)设该种商品每次降价的百分率为x,根据“两次降价后的售价=(1百分比)的平方”,即可得出关于x的一元二次方程,解方程即可得出结论;
(2)设第一次降价后售出该种商品m件,则第二次降价后售出该种商品(100m)件,根据“总利润=第一次降价后的单件利润×销售数量+第二次降价后的单件利润×销售数量”即可列出关于m的一元一次不等式,解不等式即可得出结论.
解:(1)设该种商品每次降价的百分率为x,
依题意得:400×(1-x)2=324
解得:x=0.1,或x=1.9(不合题意,舍去).
答:该种商品每次降价的百分率为10%;
(2)设第一次降价后售出该种商品m件,则第二次降价后售出该种商品(100m)件,
第一次降价后的单件利润为:400×(110%)300=60(元)
第二次降价后的单件利润为:324300=24(元)
依题意得:60m+24×(100m)≥3210,
解得:m≥22.5,
根据题意,m为整数,所以m=23
答:为使两次降价销售的总利润不少于3210元,第一次降价后至少要售出该种商品23件.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:
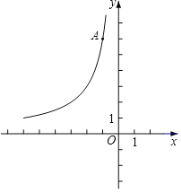
【题目】如图,在平面直角坐标系xOy中,函数y=![]() (x<0)的图象经过点A(﹣1,6).
(x<0)的图象经过点A(﹣1,6).
(1)求k的值;
(2)已知点P(a,﹣2a)(a<0),过点P作平行于x轴的直线,交直线y=﹣2x﹣2于点M,交函数y=![]() (x<0)的图象于点N.
(x<0)的图象于点N.
①当a=﹣1时,求线段PM和PN的长;
②若PN≥2PM,结合函数的图象,直接写出a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市304国道通辽至霍林郭勒段在修建过程中经过一座山峰,如图所示,其中山脚A、C两地海拔高度约为1000米,山顶B处的海拔高度约为1400米,由B处望山脚A处的俯角为30°,由B处望山脚C处的俯角为45°,若在A、C两地间打通一隧道,求隧道最短为多少米(结果取整数,参考数据![]() ≈1.732)
≈1.732)
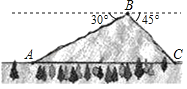
查看答案和解析>>
科目:初中数学 来源: 题型:
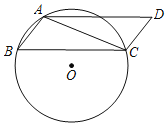
【题目】操作、证明:如图,在平行四边形ABCD中,连接AC,以点C为圆心BC为半径画弧,交△ABC的外接圆O于点E,连接AE、CE.
(1)求证:AD=CE,∠D=∠E.
(2)连接CO,求证:CO平分∠BCE.
(3)判断:“一组对边相等且一组对角相等的四边形是平行四边形”是 命题(填“真”或“假”).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 为
为![]() 边上的中线,
边上的中线,![]() 于点
于点![]()
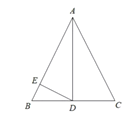
(1)求证:BD·AD=DE·AC.
(2)若AB=13,BC=10,求线段DE的长.
(3)在(2)的条件下,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,与
,与![]() 轴的
轴的![]() 个交点坐标为
个交点坐标为![]() ,
,![]() ,其部分图象如图所示,下列结论:①
,其部分图象如图所示,下列结论:①![]() ;②方程
;②方程![]() 的两个根是
的两个根是![]() ,
,![]() ;③
;③![]() ;④当
;④当![]() 时,
时,![]() 的取值范围是
的取值范围是![]() .其中结论正确的个数是( )
.其中结论正确的个数是( )
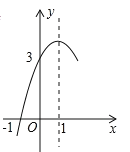
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,点E在AD上,且AE=4,点
,点E在AD上,且AE=4,点![]() 是AB上一点,连接EF,将线段EF 绕点E逆时针旋转120°得到EG,连接DG,则线段DG的最小值为____________________.
是AB上一点,连接EF,将线段EF 绕点E逆时针旋转120°得到EG,连接DG,则线段DG的最小值为____________________.
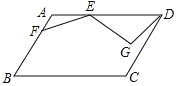
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人参加射击比赛,每人射击五次,命中的环数如下表:
次序 | 第一次 | 第二次 | 第三次 | 第四次 | 第五次 |
甲命中的环数(环) | 6 | 7 | 8 | 6 | 8 |
乙命中的环数(环) | 5 | 10 | 7 | 6 | 7 |
根据以上数据,下列说法正确的是( )
A.甲的平均成绩大于乙B.甲、乙成绩的中位数不同
C.甲、乙成绩的众数相同D.甲的成绩更稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数y=![]() (a>0,a为常数)和y=
(a>0,a为常数)和y=![]() 在第一象限内的图象如图所示,点M在y=
在第一象限内的图象如图所示,点M在y=![]() 的图象上,MC⊥x轴于点C,交y=
的图象上,MC⊥x轴于点C,交y=![]() 的图象于点A;MD⊥y轴于点D,交y=
的图象于点A;MD⊥y轴于点D,交y=![]() 的图象于点B,当点M在y=
的图象于点B,当点M在y=![]() 的图象上运动时,以下结论:
的图象上运动时,以下结论:
①S△ODB=S△OCA;
②四边形OAMB的面积不变;
③当点A是MC的中点时,则点B是MD的中点.
其中正确结论的个数是( )

A.0 B.1 C.2 D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com