Question

18．在Rt△ABC中，BC=AC，∠ACB=90°，点D为射线AB上一点，连接CD，过点C作线段CD的垂线l，在直线l上，分别在点C的两侧截取与线段CD相等的线段CE和CF，连接AE、BF．
（1）当点D在线段AB上时（点D不与点A、B重合），如图1
①请你将图形补充完整；
②线段BF、AD所在直线的位置关系为垂直，线段BF、AD的数量关系为相等；
（2）当点D在线段AB的延长线上时，如图2
①请你将图形补充完整；
②在（1）中②问的结论是否仍然成立？如果成立请进行证明，如果不成立，请说明理由．

Answer 1

分析 （1）①D在线段AB上时，在直线l上截取CE=CF=CD，即可画出图象．②在图1中证明△ACD≌△BCF得到AD=BF，∠BAC=∠FBC，利用∠ABF=∠ABC+∠FBC=∠ABC+∠BAC=90°，即BF⊥AD．
（2）①D在线段AB延长线上时，在直线l上截取CE=CF=CD，即可画出图象．②在图2中证明△ACD≌△BCF得到AD=BF，∠BAC=∠FBC，利用∠ABF=∠ABC+∠FBC=∠ABC+∠BAC=90°，即BF⊥AD．

解答 解：（1）①见图1所示．
②证明：∵CD⊥EF，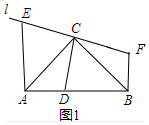
∴∠DCF=90°，
∵∠ACB=90°，
∴∠ACB=∠DCF，
∴∠ACD=∠BCF
∵BC=AC，CD=CF，
∴△ACD≌△BCF，
∴AD=BF，∠BAC=∠FBC，
∴∠ABF=∠ABC+∠FBC=∠ABC+∠BAC=90°，
即BF⊥AD．
故答案为：垂直、相等．
（2）①见图2所示．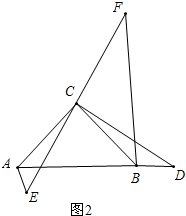
②成立．理由如下：
证明：∵CD⊥EF，
∴∠DCF=90°，
∵∠ACB=90°，
∴∠DCF+∠BCD=∠ACB+∠BCD，
即∠ACD=∠BCF，
∵BC=AC，CD=CF，
∴△ACD≌△BCF，
∴AD=BF，∠BAC=∠FBC，
∴∠ABF=∠ABC+∠FBC=∠ABC+∠BAC=90°，
即BF⊥AD．

点评 本题考查等腰直角三角形的性质、全等三角形的判定和性质、两条直线垂直的证明方法，寻找全等三角形是解决问题的关键．