
【题目】综合与探究:
(1)操作发现:如图1,在![]() 中,
中,![]() 为锐角,
为锐角,![]() 为射线
为射线![]() 上一动点,连接
上一动点,连接![]() ,以
,以![]() 为直角边且在
为直角边且在![]() 的上方作等腰直角三角形
的上方作等腰直角三角形![]() .若
.若![]() ,
,![]() .当点
.当点![]() 在线段
在线段![]() 上时(与点
上时(与点![]() 不重合),你能发现
不重合),你能发现![]() 与
与![]() 的数量关系和位置关系吗?请直接写出你发现的结论.
的数量关系和位置关系吗?请直接写出你发现的结论.

(2)类比与猜想:当点![]() 在线段
在线段![]() 的延长线上时,其余条件不变,(1)中的结论是否仍然成立?请在图2中画出相应图形并说明理由.
的延长线上时,其余条件不变,(1)中的结论是否仍然成立?请在图2中画出相应图形并说明理由.

(3)深入探究:如图3,若![]() ,
,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上运动,请写出
上运动,请写出![]() 与
与![]() 的位置关系并证明.
的位置关系并证明.

【答案】(1)![]() ,
,![]() .(2)成立,证明见解析;(3)
.(2)成立,证明见解析;(3)![]() .证明见解析
.证明见解析
【解析】
(1)根据同角的余角相等求出∠CAF=∠BAD,然后利用“边角边”证明△ACF和△ABD全等,
(2)先求出∠CAF=∠BAD,然后与(1)的思路相同求解即可;
(3)过点A作AE⊥AC交BC于E,可得△ACE是等腰直角三角形,根据等腰直角三角形的性质可得AC=AE,∠AED=45°,再根据同角的余角相等求出∠CAF=∠EAD,然后利用“边角边”证明△ACF和△AED全等,根据全等三角形对应角相等可得∠ACF=∠AED,然后求出∠BCF=90°,从而得到CF⊥BD.
解:∵![]() ,
,![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,![]() ,
,
∴![]() .
.
在![]() 和
和![]() 中,
中,
![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)成立.
证明:如图2,
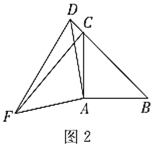
∵![]() ,
,
∴![]() ,
,
即![]() .
.
在![]() 和
和![]() 中,
中,
![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(3)![]() .
.
证明:如图3,过点![]() 作
作![]() 交
交![]() 于
于![]() .
.
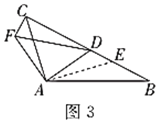
∵![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】某公司根据市场计划调整投资策略,对![]() ,
,![]() 两种产品进行市场调查,收集数据如表:
两种产品进行市场调查,收集数据如表:
项目 产品 | 年固定成本 (单位:万元) | 每件成本 (单位:万元) | 每件产品销售价 (万元) | 每年最多可生产的件数 |
|
|
|
|
|
|
|
|
|
|
其中![]() 是待定常数,其值是由生产
是待定常数,其值是由生产![]() 的材料的市场价格决定的,变化范围是
的材料的市场价格决定的,变化范围是![]() ,销售
,销售![]() 产品时需缴纳
产品时需缴纳![]() 万元的关税,其中
万元的关税,其中![]() 为生产产品的件数,假定所有产品都能在当年售出,设生产
为生产产品的件数,假定所有产品都能在当年售出,设生产![]() ,
,![]() 两种产品的年利润分别为
两种产品的年利润分别为![]() 、
、![]() (万元),写出
(万元),写出![]() 、
、![]() 与
与![]() 之间的函数关系式,注明其自变量
之间的函数关系式,注明其自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家实行一系列“三农”优惠政策后,农民收入大幅度增加.某乡所辖村庄去年的年人均收入(单位:元)情况如下表:
年人均收入 | 3 500 | 3 700 | 3 800 | 3 900 | 4 500 |
村庄个数 | 1 | 1 | 3 | 3 | 1 |
该乡去年各村庄年人均收入的中位数是( )
A.3 700元B.3 800元C.3 850元D.3 900元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山西皮影戏又称“影戏”或“影子戏”,属于传统民间艺术,皮影是一种以兽皮或纸板做成的人物剪影,在制作人物剪影中,给出下面4个条件:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.

(1)在上述四个条件中,选三个条件作为题设,另一个作为结论,其中真命题有哪几个?(用序号表示即可)
(2)请选择(1)中的一个命题证明其正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:
我们知道“两边及其中一边的对角分别对应相等的两个三角形不一定全等”.但是,乐乐发现:当这两个三角形都是锐角三角形时,它们会全等.
(1)请你用所学知识判断乐乐说法的正确性.
如图,已知![]() 、
、![]() 均为锐角三角形,且
均为锐角三角形,且![]() ,
,![]() ,
,![]() .
.
求证:![]() .
.

(2)除乐乐的发现之外,当这两个三角形都是______时,它们也会全等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为![]() 的正方形
的正方形![]() 的顶点
的顶点![]() 、
、![]() 在一个半径为
在一个半径为![]() 的圆上,顶点
的圆上,顶点![]() 、
、![]() 在圆内,将正方形
在圆内,将正方形![]() 沿圆的内壁逆时针方向作无滑动的滚动.当点
沿圆的内壁逆时针方向作无滑动的滚动.当点![]() 第一次落在圆上时,点
第一次落在圆上时,点![]() 运动的路径长为________.
运动的路径长为________.
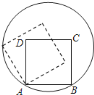
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx﹣3的图象经过点A,且函数值y随x的增大而增大,则点A的坐标不可能是( )
A.(﹣2,﹣4)B.(﹣1,2)C.(5,1)D.(﹣1,﹣4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC与BD相交于点O,∠DAB=∠CBA,添加下列哪一个条件后,仍不能使△ADB≌△CBA的是( )

A.AD=BCB.∠ABD=∠BACC.OA=OBD.AC=BD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com