
分析 先通分,再算减法,化成最简,最后把x=2$\sqrt{2}$-2代入计算即可.
解答 解:原式=$\frac{(x+2)(x-2)}{x+2}$-$\frac{{x}^{2}}{x+2}$
=$\frac{{x}^{2}-4}{x+2}$-$\frac{{x}^{2}}{x+2}$
=$\frac{{x}^{2}-4-{x}^{2}}{x+2}$
=-$\frac{4}{x+2}$,
当x=2$\sqrt{2}$-2时,
原式=-$\frac{4}{2\sqrt{2}-2+2}$
=-$\frac{4}{2\sqrt{2}}$
=-$\sqrt{2}$.
点评 本题考查了分式的化简求值,特别注意运算顺序及符号的处理,也需要对通分、分解因式、约分等知识点熟练掌握.


科目:初中数学 来源: 题型:填空题
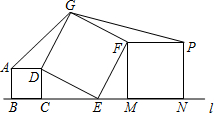 在平面内,按图摆放着三个正方形ABCD、DEFG和MNPF,其中点B、C、E、M、N依次位于直线l上.已知正方形ABCD的面积为4,正方形DEFG的面积为13,则△ADG的面积为$\sqrt{6}$.
在平面内,按图摆放着三个正方形ABCD、DEFG和MNPF,其中点B、C、E、M、N依次位于直线l上.已知正方形ABCD的面积为4,正方形DEFG的面积为13,则△ADG的面积为$\sqrt{6}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在正方形ABCD中,P是对角线AC上的一点,点E在BC的延长线上,且PE=PB.
如图,在正方形ABCD中,P是对角线AC上的一点,点E在BC的延长线上,且PE=PB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com