
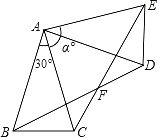
【题目】如图,△ABC中,AB=AC,∠BAC=30°,将△ABC绕点A按逆时针方向旋转α°.得到△ADE,连接BD,CE交于点F.
(1)求证:△ABD≌△ACE;
(2)用α表示∠ACE的度数;
(3)若使四边形ABFE是菱形,求α的度数.
【答案】(1)证明见解析;(2)∠ACE==90°﹣![]() ;(3)120°.
;(3)120°.
【解析】
(1)根据旋转角求出∠BAD=∠CAE,然后利用“边角边”证明△ABD和△ACE全等;
(2)根据等腰三角形的性质得到结论;
(3)根据等腰三角形的性质得到∠ABD=∠ADB=∠ACE=∠AEC=90°﹣![]() ,求得∠BFE=150°,若使四边形ABFE是菱形,只要四边形ABFE是平行四边形即可,得到∠BAE=∠BFE,于是得到结论.
,求得∠BFE=150°,若使四边形ABFE是菱形,只要四边形ABFE是平行四边形即可,得到∠BAE=∠BFE,于是得到结论.
解:(1)证明:∵ABC绕点A按逆时针方向旋转α°,
∴∠BAC=∠DAE=30°,∠BAD=∠CAE=α°,
又∵AB=AC,
∴AB=AC=AD=AE,
在△ABD与△ACE中,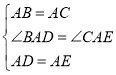 ,
,
∴△ABD≌△ACE(SAS);
(2)解:∵∠CAE=α°,AC=AE,
∴∠ACE=![]() (180°﹣∠CAE)=
(180°﹣∠CAE)=![]() (180°﹣α°)=90°﹣
(180°﹣α°)=90°﹣![]() ;
;
(3)解:∵∠BAD=∠CAE=α°,AB=AC=AD=AE,
∴∠ABD=∠ADB=∠ACE=∠AEC=90°﹣![]() ,
,
∵∠BAE=∠BAD+∠DAE=α°+30°=(α+30)°,
∴∠BFE=360°﹣∠BAE﹣∠ABD﹣∠AEC=360°﹣(α+30)°﹣2(90°﹣![]() )=150°,
)=150°,
∵AB=AE,
∴若使四边形ABFE是菱形,
只要四边形ABFE是平行四边形即可,
∵∠ABD=∠AEC,
∴只要∠BAE=∠BFE,
即(30+α)°=150°,
解得:α°=120°,
即当α°=120°时,四边形ABFE是菱形.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:
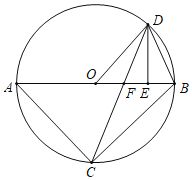
【题目】如图,已知△ABC内接于⊙O,AB是直径,点D在⊙O上,OD∥BC,过点D作DE⊥AB,垂足为E,连接CD交OE边于点F.
(1)求证:△DOE∽△ABC;
(2)求证:∠ODF=∠BDE;
(3)连接OC.设△DOE的面积为S.sinA=![]() ,求四边形BCOD的面积(用含有S的式子表示)
,求四边形BCOD的面积(用含有S的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
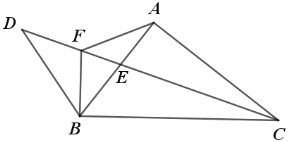
【题目】如图,Rt△ABC 中,∠BAC=90°,CE 平分∠ACB,点 D 在 CE的延长线上,连接 BD,过B作BF⊥BC交 CD 于点 F,连接 AF,若CF=2BD ,DE:CE=5:8 , BF ![]() ,则AF的长为_________.
,则AF的长为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】疫情期间,“线上教学”为我们提供了复习的渠道.学校随机抽取部分学生就“你是否喜欢线上教学”进行了问卷调查,并将调查结果统计后绘制成如下统计表和统计图.
调查结果统计表
类别 | 非常喜欢 | 喜欢 | 一般 | 不喜欢 |
频数 | a | 70 | 20 | 10 |
频率 | 0.5 | b | 0.15 | |
调查结果扇形统计图

(1)在统计表中,a= ;b= ;
(2)在扇形统计图中,对线上教学感觉“一般”所对应的圆心角度数为 ;
(3)已知全校共有3000名学生,试估计“喜欢”线上教学的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一边长为10m的等边△ABC游乐场,某人从边AB中点P出发,先由点P沿平行于BC的方向运动到AC边上的点P1,再由P1沿平行于AB方向运动到BC边上的点P2,又由点P2沿平行于AC方向运动到AB边上的点P3,则此人至少要运动_____m,才能回到点P.如果此人从AB边上任意一点出发,按照上面的规律运动,则此人至少走_____m,就能回到起点.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系![]() 中的图形
中的图形![]() ,
,![]() ,给出如下定义:
,给出如下定义:![]() 为图形
为图形![]() 上任意一点,
上任意一点,![]() 为图形
为图形![]() 上任意一点,如果线段
上任意一点,如果线段![]() 的长度有最小值,那么称这个最小值为图形
的长度有最小值,那么称这个最小值为图形![]() ,
,![]() 的“近距”,记作
的“近距”,记作![]() ;如果线段
;如果线段![]() 的长度有最大值,那么称这个最大值为图形
的长度有最大值,那么称这个最大值为图形![]() ,
,![]() 的“远距”,记作
的“远距”,记作![]() .
.
已知点![]() ,
,![]() .
.
(1)![]() (点
(点![]() ,线段
,线段![]() )
)![]() ______,
______,![]() (点
(点![]() ,线段
,线段![]() )
)![]() ______;
______;
(2)一次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() (线段
(线段![]() ,线段
,线段![]() )
)![]() ,
,
①求![]() 的值;
的值;
②直接写出![]() (线段
(线段![]() ,线段
,线段![]() )
)![]() ______;
______;
(3)![]() 的圆心为
的圆心为![]() ,半径为1.若
,半径为1.若![]() (
(![]() 线段
线段![]() )
)![]() ,请直接写出
,请直接写出![]() (
(![]() ,线段
,线段![]() )的取值范围.
)的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直角三角形![]() 的直角顶点
的直角顶点![]() 在矩形
在矩形![]() 的对角线
的对角线![]() 上(点
上(点![]() 不与点
不与点![]() 重合,可与点
重合,可与点![]() 重合),满足
重合),满足![]() ,
,![]() 于点
于点![]() ,已知
,已知![]() ,
,![]() .
.
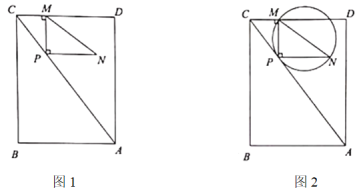
(1)若![]() ,则
,则![]() ___________;
___________;
(2)当点![]() 在
在![]() 的平分线上时,求
的平分线上时,求![]() 的长;
的长;
(3)当点![]() 的位置发生改变时:
的位置发生改变时:
①如图2,![]() 的外接圆是否与
的外接圆是否与![]() 一直保持相切.说明理由;
一直保持相切.说明理由;
②直接写出![]() 的外接圆与
的外接圆与![]() 相切时
相切时![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E.在△ABC外有一点F,使FA⊥AE,FC⊥BC.
(1)求证:BE=CF;
(2)在AB上取一点M,使BM=2DE,连接MC,交AD于点N,连接ME.求证:①ME⊥BC;②DE=DN.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com