
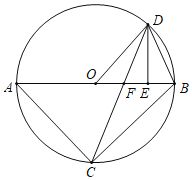
【题目】如图,已知△ABC内接于⊙O,AB是直径,点D在⊙O上,OD∥BC,过点D作DE⊥AB,垂足为E,连接CD交OE边于点F.
(1)求证:△DOE∽△ABC;
(2)求证:∠ODF=∠BDE;
(3)连接OC.设△DOE的面积为S.sinA=![]() ,求四边形BCOD的面积(用含有S的式子表示)
,求四边形BCOD的面积(用含有S的式子表示)
【答案】(1)见解析;(2)见解析;(3)S四边形BCOD=![]() .
.
【解析】
(1)根据圆周角定理和垂直(DE⊥AB)得出∠DEO=∠ACB;根据平行(OD∥BC)得出∠DOE=∠ABC;根据相似三角形的判定即可证明;
(2)根据相似三角形的性质可得∠ODE=∠A,根据圆周角定理可得∠A=∠BDC,进而推出∠ODE=∠BDC,等式两边同时减去∠EDF即可证明∠ODF=∠BDE.
(3)根据相似三角形的性质可得S△ABC=4S△DOE=4S,进而可得S△BOC=2S;由sinA=![]() ,∠A=∠ODE及圆的半径相等(OD=OB),可得
,∠A=∠ODE及圆的半径相等(OD=OB),可得![]() ,将三部分的面积相加,即可解答本题.
,将三部分的面积相加,即可解答本题.
(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∵DE⊥AB,
∴∠DEO=90°,
∴∠DEO=∠ACB,
∵OD∥BC,
∴∠DOE=∠ABC,
∴△DOE∽△ABC;
(2)证明:∵△DOE∽△ABC,
∴∠ODE=∠A,
∵∠A和∠BDC是![]() 所对的圆周角,
所对的圆周角,
∴∠A=∠BDC,
∴∠ODE=∠BDC,
∴∠ODF=∠BDE;
(3)解:∵△DOE∽△ABC,
∴![]() ,
,
即S△ABC=4S△DOE=4S,
∵OA=OB,
∴![]() ,
,
即S△BOC=2S,
∵sinA=![]() ,sinA=sin∠ODE,
,sinA=sin∠ODE,
∴![]() ,
,
∴OE=![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴S四边形BCOD=S△BOC+S△DOE+![]() .
.


科目:初中数学 来源: 题型:
【题目】某单位计划从商店购买同一种品牌的钢笔和笔记本,已知购买一支钢笔比购买一个笔记本多用20元,若用1500元购买钢笔和用600元购买笔记本,则购买钢笔的数量是购买笔记本数量的一半.
(1)求购买一支钢笔、一个笔记本各需要多少元?
(2)经商谈,商店给予优惠,优惠方式是每购买一支钢笔赠送一个笔记本;如果此单位需要笔记本的数量是钢笔数量的3倍还少6个,且购买钢笔和笔记本的总费用不超过1020元,那么最多可购买多少支钢笔?
查看答案和解析>>
科目:初中数学 来源: 题型:
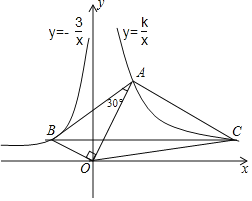
【题目】如图,已知∠AOB=90°,∠OAB=30°,反比例函数![]() 的图象过点
的图象过点![]() ,反比例函数
,反比例函数![]() 的图象过点A
的图象过点A
(1)求![]() 和
和![]() 的值.
的值.
(2)过点B作BC∥x轴,与双曲线![]() 交于点C,求△OAC的面积.
交于点C,求△OAC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
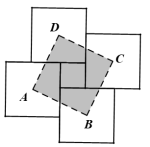
【题目】用四块大正方形地砖和一块小正方形地砖拼成如图所示的实线图案,每块大正方形地砖面积为a,小正方形地砖面积为依次连接四块大正方形地砖的中心得到正方形ABCD.则正方形ABCD的面积为____________(用含a,b的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数![]() b,c是常数,
b,c是常数,![]() 图象的一部分,与x轴的交点A在点
图象的一部分,与x轴的交点A在点![]() 和
和![]() 之间,对称轴是
之间,对称轴是![]() 对于下列说法:
对于下列说法:![]() ;
;![]() ;
;![]() ;
;![]() 为实数);(5)当
为实数);(5)当![]() 时,
时,![]() ,其中正确的是( )
,其中正确的是( )

A.(1)(2)(4)B.(1)(2)(5)C.(2)(3)(4)D.(3)(4)(5)
查看答案和解析>>
科目:初中数学 来源: 题型:
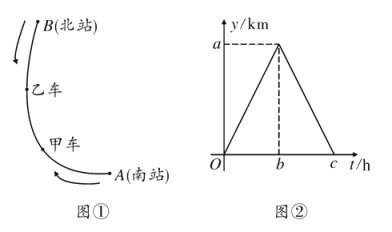
【题目】如图①,长为120 km的某段线路AB上有甲、乙两车,分别从南站A和北站B同时出发相向而行,到达B,A后立刻返回到出发站停止,速度均为40 km/h,设甲车,乙车距南站A的路程分别为y甲,y乙(km),行驶时间为t(h).
(1)图②已画出y甲与t的函数图象,其中a=____,b=____,c=____;
(2)分别写出0≤t≤3及3<t≤6时,y乙与时间t之间的函数关系式;
(3)在图②中补画y乙与t之间的函数图象,并观察图象计算出在整个行驶过程中两车相遇的次数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正比例函数y1的图象与反比例函数y2的图象相交于点A(2,-4),下列说法正确的是( )
A.反比例函数y2的解析式是![]()
B.两个函数图象的另一交点坐标为(2,4)
C.当x<-2或0<x<2时,y1>y2
D.正比例函数y1与反比例函数y2都随x的增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:
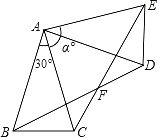
【题目】如图,△ABC中,AB=AC,∠BAC=30°,将△ABC绕点A按逆时针方向旋转α°.得到△ADE,连接BD,CE交于点F.
(1)求证:△ABD≌△ACE;
(2)用α表示∠ACE的度数;
(3)若使四边形ABFE是菱形,求α的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com