
 如图,D是∠BAC角平分线上异于A的一点,B、C分别是∠BAC两边上异于A的任意一点,连接DB和DC,分别增加下列条件后,仍不能判定△ADB≌△ADC的是( )
如图,D是∠BAC角平分线上异于A的一点,B、C分别是∠BAC两边上异于A的任意一点,连接DB和DC,分别增加下列条件后,仍不能判定△ADB≌△ADC的是( )| A、AB=AC |
| B、DC=DB |
| C、∠ACD=∠ABD |
| D、∠ADC=∠ADB |
 解:如图,∵D是∠BAC角平分线上异于A的一点,
解:如图,∵D是∠BAC角平分线上异于A的一点,

 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:
| A、平行四边形的对边相等 |
| B、四条边都相等的四边形是菱形 |
| C、矩形的两条对角线互相垂直 |
| D、对角线互相平分的四边形是平行四边形 |
查看答案和解析>>
科目:初中数学 来源: 题型:
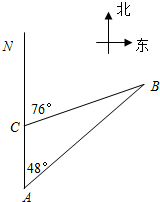 如图,一艘货轮以30海里/时的速度在海面上航行,当它行驶到A处时,发现在它的北偏东48°方向有一港口B,货轮继续向北航行40分钟后到达C处,发现港口B在它的北偏东76°方向上,若货轮急需到港口B补充供给,请求出C处与港口B的距离CB的长度.(结果保留整数)
如图,一艘货轮以30海里/时的速度在海面上航行,当它行驶到A处时,发现在它的北偏东48°方向有一港口B,货轮继续向北航行40分钟后到达C处,发现港口B在它的北偏东76°方向上,若货轮急需到港口B补充供给,请求出C处与港口B的距离CB的长度.(结果保留整数)| 20 |
| 21 |
| 10 |
| 9 |
| 4 |
| 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com