
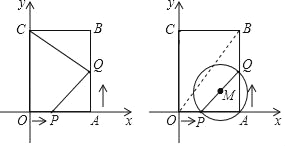
【题目】如图,四边形OABC是矩形,点A的坐标为(3,0),点C的坐标为(0,6),点P从点O出发,沿OA以每秒1个单位长度的速度向点A出发,同时点Q从点A出发,沿AB以每秒2个单位长度的速度向点B运动,当点P与点A重合时运动停止.设运动时间为t秒.
(1)当t=2时,线段PQ的中点坐标为 .
(2)当△CBQ与△PAQ相似时,求t的值;
(3)连接OB,若以PQ为直径作⊙M,则在运动过程中,是否存在某一时刻t,使得⊙M与OB相切,若存在,求出时间t;若不存在,请说明理由.
【答案】(1)(![]() ,2);(2)t的值为
,2);(2)t的值为![]() 或
或![]() ;(3)在运动过程中,存在某一时刻t,使得⊙M与OB相切,此时t的值为
;(3)在运动过程中,存在某一时刻t,使得⊙M与OB相切,此时t的值为![]() .
.
【解析】
(1)根据点P,Q的运动速度找出当t=2时,点P,Q的坐标,再利用中点坐标公式即可求出此时线段PQ的中点坐标;
(2)根据点P,Q的运动速度找出运动时间为t秒时,PA,QA,QB,CB的值,由∠B=∠A=90°,可得出当![]() 时,△CBQ与△PAQ相似,代入各线段的值即可求出t值;
时,△CBQ与△PAQ相似,代入各线段的值即可求出t值;
(3)找出当运动时间为t(0≤t≤3)秒时点M的坐标,进而可得出点M在直线y=2x﹣3上,设直线y=2x﹣3与x轴交于点E,与线段AB交于点F,利用一次函数图象上点的坐标特征可求出点F的坐标,由矩形的性质结合点A,C的坐标可得出点B的坐标,进而可得出直线OB的解析式,结合直线EF的解析式可得出EF∥OB,过点A作AD⊥OB于点D,AD交直线EF于点M,则点M为线段AD的中点,此时⊙M与OB相切.由直线OB的解析式、AD⊥OB结合点A的坐标可得出直线AD的解析式,联立直线AD,EF的解析式成方程组,通过解方程组可求出M的坐标,由点M的纵坐标可得出t的值,此题得解.
解:(1)当t=2时,点P的坐标为(2,0),点Q的坐标为(3,4),
∴线段PQ的中点坐标为(![]() ),即(
),即(![]() ,2).
,2).
故答案为:(![]() ,2).
,2).
(2)当运动时间为t(0≤t≤3)秒时,点P的坐标为(t,0),点Q的坐标为(3,2t),
∴PA=3﹣t,QA=2t,QB=6﹣2t,CB=3.
∵∠B=∠A=90°,
∴当![]() 时,△CBQ与△PAQ相似.
时,△CBQ与△PAQ相似.
当![]() 时,
时,![]() ,
,
解得:t1=![]() ,t2=
,t2=![]() (不合题意,舍去);
(不合题意,舍去);
当![]() 时,
时,![]() ,
,
解得:t=![]() .
.
综上所述:t的值为![]() 或
或![]() .
.
(3)当运动时间为t(0≤t≤3)秒时,点P的坐标为(t,0),点Q的坐标为(3,2t),
∴点M的坐标为(![]() ,t).
,t).
∵t=![]() ×2﹣3,
×2﹣3,
∴点M在直线y=2x﹣3上.
设直线y=2x﹣3与x轴交于点E,与线段AB交于点F,则点F的坐标为(3,3),
∴点F为线段AB的中点.
∵四边形OABC是矩形,点A的坐标为(3,0),点C的坐标为(0,6),
∴点B的坐标为(3,6),
∴直线OB的解析式为y=2x,
∴直线OB∥直线EF.
过点A作AD⊥OB于点D,AD交直线EF于点M,如图所示.
∵直线OB∥直线EF,
∴MF为△ABD的中位线,
∴点M为线段AD的中点,
∴此时⊙M与OB相切.
∵AD⊥OB,点A的坐标为(3,0),
∴直线AD的解析式为y=﹣![]() (x﹣3),即y=﹣
(x﹣3),即y=﹣![]() x+
x+![]() .
.
联立直线AD,EF的解析式成方程组,得:
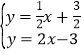 ,解得:
,解得:![]() ,
,
∴点M的坐标为(![]() ,
,![]() ),
),
∴t=![]() ,
,
∴在运动过程中,存在某一时刻t,使得⊙M与OB相切,此时t的值为![]() .
.


科目:初中数学 来源: 题型:
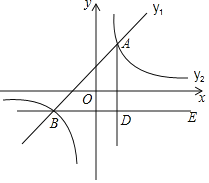
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() 和
和![]() .
.
![]() 求一次函数和反比例函数的表达式;
求一次函数和反比例函数的表达式;
![]() 请直接写出
请直接写出![]() 时,x的取值范围;
时,x的取值范围;
![]() 过点B作
过点B作![]() 轴,
轴,![]() 于点D,点C是直线BE上一点,若
于点D,点C是直线BE上一点,若![]() ,求点C的坐标.
,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里有 ![]() 个除颜色外都相同的球,其中有
个除颜色外都相同的球,其中有 ![]() 个红球,
个红球, ![]() 个黄球.
个黄球.
(1) 若从中随意摸出一个球,求摸出红球的可能性;
(2) 若要使从中随意摸出一个球是红球的可能性为 ![]() ,求袋子中需再加入几个红球?
,求袋子中需再加入几个红球?
查看答案和解析>>
科目:初中数学 来源: 题型:
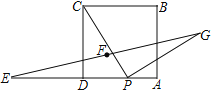
【题目】如图,正方形ABCD的边长为4,点E为AD的延长线上一点,且DE=DC,点P为边AD上一动点,且PC⊥PG,PG=PC,点F为EG的中点.当点P从D点运动到A点时,则CF的最小值为___________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】热气球的探测器显示,从热气球底部A处看一栋高楼顶部的俯角为30°,看这栋楼底部的俯角为60°,热气球A处与地面距离为420米,求这栋楼的高度.
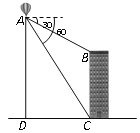
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形OABC的顶点O,B在y轴上,顶点A在反比例函数y=![]() 上,顶点C在反比例函数y=
上,顶点C在反比例函数y=![]() 上,则平行四边形OABC的面积是____________.
上,则平行四边形OABC的面积是____________.
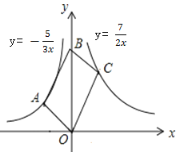
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x+2与x轴交于点A,与y轴交于点B,抛物线y=﹣
x+2与x轴交于点A,与y轴交于点B,抛物线y=﹣![]() x2+bx+c经过A、B两点,与x轴的另一个交点为 C.
x2+bx+c经过A、B两点,与x轴的另一个交点为 C.
(1)求抛物线的解析式;
(2)直线AB上方抛物线上的点D,使得∠DBA=2∠BAC,求D点的坐标;
(3)M是平面内一点,将△BOC绕点M逆时针旋转90°后,得到△B1O1C1,若△B1O1C1的两个顶点恰好落在抛物线上,请求点B1的坐标.
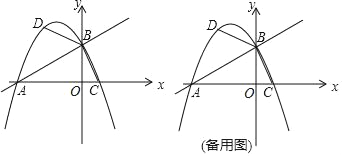
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,小明准备测量学校旗杆AB的高度,他发现阳光下,旗杆AB的影子恰好落在水平地面和斜坡的坡面上,测得水平地面上的影长BC=20m,斜坡坡面上的影长CD=8m,太阳光线AD与水平地面成锐角为26°,斜坡CD与水平地面所成的锐角为30°,求旗杆AB的高度(精确到1m).(参考数据:sin26°=0.44,cos26°=0.90,tan26°=0.49)
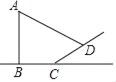
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com