
【题目】如图,广场中心菱形花坛ABCD的周长是32米,∠A=60°,则A、C两点之间的距离为( )
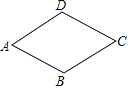
A. 4米 B. ![]() 米 C. 8米 D.
米 C. 8米 D. ![]() 米
米
 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:
【题目】如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM,下面结论:
①△ABE≌△DBC;②∠DMA=60°;③△BPQ为等边三角形;④MB平分∠AMC,
其中结论正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 要了解某公司生产的100万只灯泡的使用寿命,可以采用抽样调查的方法
B. 4位同学的数学期末成绩分别为100、95、105、110,则这四位同学数学期末成绩的中位数为100
C. 甲乙两人各自跳远10次,若他们跳远成绩的平均数相同,甲乙跳远成绩的方差分别为0.51和0.62,则乙的表现较甲更稳定
D. 某次抽奖活动中,中奖的概率为![]() 表示每抽奖50次就有一次中奖
表示每抽奖50次就有一次中奖
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 分别与
分别与![]() 轴,
轴,![]() 轴交于
轴交于![]() 两点,与直线
两点,与直线![]() 交于点
交于点![]() .
.
(1)点![]() 的坐标为__________,点
的坐标为__________,点![]() 的坐标为__________
的坐标为__________
(2)在线段![]() 上有一点
上有一点![]() ,过点
,过点![]() 作
作![]() 轴的平行线
轴的平行线![]() 交直线
交直线![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,当
,当![]() 为何值时,四边形
为何值时,四边形![]() 是平行四边形.
是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
有这样一个问题:关于x 的一元二次方程a x2+bx+c=0(a>0)有两个不相等的且非零的实数根.探究a,b,c满足的条件.
小明根据学习函数的经验,认为可以从二次函数的角度看一元二次方程,下面是小明的探究过程:
①设一元二次方程ax2+bx+c=0(a>0)对应的二次函数为y=ax2+bx+c(a>0);
②借助二次函数图象,可以得到相应的一元二次中a,b,c满足的条件,列表如下:
方程根的几何意义:请将(2)补充完整
方程两根的情况 | 对应的二次函数的大致图象 | a,b,c满足的条件 |
方程有两个 不相等的负实根 |
|
|
_____ |
|
|
方程有两个 不相等的正实根 | _____ | _____ |
(1)参考小明的做法,把上述表格补充完整;
(2)若一元二次方程mx2﹣(2m+3)x﹣4m=0有一个负实根,一个正实根,且负实根大于﹣1,求实数m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
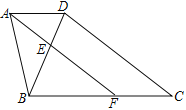
【题目】如图,在四边形ABCD中,AD∥BC,AB=3,BC=5,连接BD,∠BAD的平分线分别交BD、BC于点E、F,且AE∥CD
(1) 求AD的长;
(2) 若∠C=30°,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,∠A=90°,点P.Q分別是AB、AC上的动点,且满足BP=AQ,D是BC的中点,当点P运动到___时,四边形APDQ是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
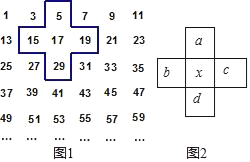
【题目】如图,将连续的奇数1,3,5,7…按图1中的方式排成一个数表,用一个十字框框住5个数,这样框出的任意5个数(如图2)分别用a,b,c,d,x表示.
(1)若x=17,则a+b+c+d= .
(2)移动十字框,用x表示a+b+c+d= .
(3)设M=a+b+c+d+x,判断M的值能否等于2020,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,点E、F、G分别为边AB、BC、CD的中点,若△EFG的面积为4,则四边形ABCD的面积为( )
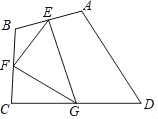
A. 8 B. 12 C. 16 D. 18
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com