练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．某种禽流感病毒的直径为0.000000012米，将这个数用科学记数法表示为1.2×10-8米．

    分析 绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10-n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．

    解答 解：0.000000012=1.2×10-8米，
    故答案为：1.2×10-8．

    点评 本题考查用科学记数法表示较小的数，一般形式为a×10-n，其中1≤|a|＜10，n为由原数左边起第一个不为零的数字前面的0的个数所决定．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    12．铜仁市碧江区组织开展“吸烟有害健康”的知识竞赛，共25道题，选对一题得4分，不选或选错扣2分，得分不低于60分获奖，那么获奖至少选对19道题．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．若$\sqrt{2m+n}$与$\root{m-n-1}{m+5}$是同类二次根式，则$\sqrt{m+n}$的值为（　　）
    A．1B．4C．5D．$\sqrt{5}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．一次函数y=$\frac{\sqrt{3}}{3}$x+2的图象与x轴、y轴分别交于点A、B，以AB为边在第二象限内作等边△ABC．
    （1）求C点坐标；
    （2）在第二象限内有一点M（m，1），使S△ABC=S△ABM，求M点坐标；
    （3）点C′（2$\sqrt{3}$，0），在直线AB上是否存在一点P，使△ACP为等腰三角形？若存在，求P点坐标；若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    17．如图，在Rt△ABC，∠C=90°，BC=3厘米，AC=4厘米．将△ABC沿BC方向平移1厘米，得到△A′B′C′，则四边形ABC′A′的面积为10平方厘米．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

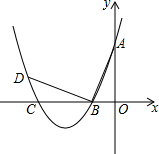    7．如图，在平面直角坐标系中．顶点为（-4，-1）的抛物线交y轴于点A（0，3），交x轴于B，C两点．
    （1）求此抛物线的解析式；
    （2）已知点P是抛物线上位于B，C两点之间的一个动点，问：当点P运动到什么位置时，四边形ABPC的面积最大？并求出此时四边形ABPC的面积．
    （3）过点B作AB的垂线交抛物线于点D，是否存在以点C为圆心且与线段BD和抛物线的对称轴l同时相切的圆？若存在，求出圆的半径；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．若二次函数y=-x2+3x+m的图象全部在x轴的下方，则m的取值范围为m＜-$\frac{9}{4}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

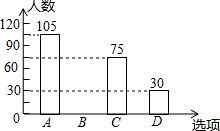    11．某校决定在6月8日“世界海洋日”开展系列海洋知识的宣传活动，活动有A．唱歌、B．舞蹈、C．绘画、D．演讲四项宣传方式．学校围绕“你最喜欢的宣传方式是什么？”在全校学生中进行随机抽样调查（四个选项中必选且只选一项），根据调查统计结果，绘制了如下两种不完整的统计图表：
    选项方式百分比
    A唱歌35%
    B舞蹈a
    C绘画25%
    D演讲10%
    请结合统计图表，回答下列问题：
    （1）本次抽查的学生共300人，a=30%，并将条形统计图补充完整；
    （2）如果该校学生有1800人，请你估计该校喜欢“唱歌”这项宣传方式的学生约有多少人？
    （3）学校采用抽签方式让每班在A、B、C、D四项宣传方式中随机抽取两项进行展示，请用树状图或列表法求某班所抽到的两项方式恰好是“唱歌”和“舞蹈”的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．如图，A，B，C三点的坐标分别为（3，1），（1，2），（0，$\sqrt{3}$），试求四边形OABC的面积．

    查看答案和解析>>

    同步练习册答案