
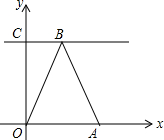
 在直角梯形OABC中,CB∥OA,∠COA=90°,CB=3,OA=6,BA=3$\sqrt{5}$,分别以OA,OC边所在直线为x轴、y轴建立如图所示的平面直角坐标系;
在直角梯形OABC中,CB∥OA,∠COA=90°,CB=3,OA=6,BA=3$\sqrt{5}$,分别以OA,OC边所在直线为x轴、y轴建立如图所示的平面直角坐标系;分析 (1)过B作BH⊥x轴于H,则OH=BC=3,进而可求得AH的长,在Rt△ABH中,根据勾股定理即可求出BH的长,由此可得B点坐标;
(2)过点B作BH⊥OA,垂足为H,过点E作EF⊥OA,垂足为F.由HB∥EF可知$\frac{EF}{BH}=\frac{AF}{AH}=\frac{4}{9}$,从而可求得:EF=$\frac{8}{3}$,AF=$\frac{4}{3}$,故此可求得点E的坐标为($\frac{14}{3}$,$\frac{8}{3}$),由题意可知点D的坐标为(0,5),最后依据待定系数法可求得直线DE的解析式y=-$\frac{1}{2}$x+5;
(3)由菱形的性质可知MB=MC或CM=BC或BM=CM,然后依据线段垂直平分线的性质和两点之间的距离公式列方程求解即可.
解答 解:(1)如图1所示:作BH⊥x轴于点H.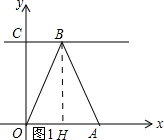
∵∠COH=∠OCB=∠BHO=90°,
∴四边形OHBC为矩形.
∴OH=CB=3.
∴AH=OA-OH=6-3=3.
在Rt△ABH中,BH=$\sqrt{B{A}^{2}-A{H}^{2}}=\sqrt{(3\sqrt{5})^{2}-{3}^{2}}=6$,
∴点B的坐标为(3,6);
(2)如图2所示:过点B作BH⊥OA,垂足为H,过点E作EF⊥OA,垂足为F.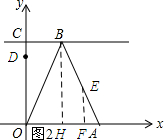
∵BH⊥OA,EF⊥OA,
∴BH∥EF.
∴$\frac{EF}{BH}=\frac{AF}{AH}=\frac{4}{9}$,即$\frac{EF}{6}=\frac{AF}{3}=\frac{4}{9}$.
解得:EF=$\frac{8}{3}$,AF=$\frac{4}{3}$.
∴OF=OA-AF=6-$\frac{4}{3}$=$\frac{14}{3}$.
∴点E的坐标为($\frac{14}{3}$,$\frac{8}{3}$).
∵OD=5,
∴点D的坐标为(0,5).
设DE的解析式为y=kx+b.将点D、E的坐标代入得:$\left\{\begin{array}{l}{\frac{14}{3}k+b=\frac{8}{3}}\\{b=5}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=5}\end{array}\right.$.
∴直线DE的解析式为:y=-$\frac{1}{2}$x+5;
(3)存在.
①如图3所示:点M在BC的垂直平分线上.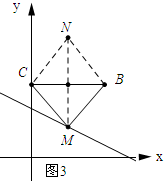
∵将x=$\frac{3}{2}$,代入y=-$\frac{1}{2}x+5$得:y=$\frac{17}{4}$.
∴点M的坐标为($\frac{3}{2}$,$\frac{17}{4}$).
如图4、如图5所示:当CM=BC时.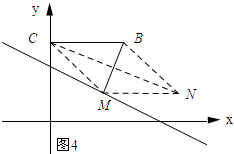
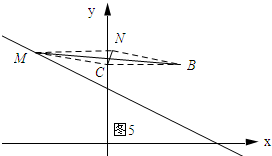
设点M的坐标为(x,-$\frac{1}{2}x+5$),由两点间的距离公式可知:$\sqrt{(x-0)^{2}+(-\frac{1}{2}x+5-6)^{2}}$=3.
整理得:5x2+4x-32=0.
解得:${x}_{1}=\frac{-2+2\sqrt{41}}{5}$,${x}_{2}=\frac{-2-2\sqrt{41}}{5}$.
将x=$\frac{-2+2\sqrt{41}}{5}$代入y=-$\frac{1}{2}x+5$得:y=$\frac{26-\sqrt{41}}{5}$,
将x=$\frac{-2-2\sqrt{41}}{5}$代入y=-$\frac{1}{2}x+5$得:y=$\frac{26+\sqrt{41}}{5}$.
∴点M的坐标为($\frac{-2+2\sqrt{41}}{5}$,$\frac{26-\sqrt{41}}{5}$)或($\frac{-2-2\sqrt{41}}{5}$,$\frac{26+\sqrt{41}}{5}$).
如图6、图7所示:BM=CM.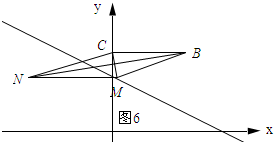
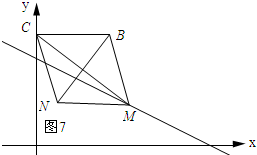
设点M的坐标为(x,-$\frac{1}{2}x+5$),由两点间的距离公式可知:$\sqrt{(x-3)^{2}+(-\frac{1}{2}x+5-6)^{2}}$=3.
整理得:5x2-20x+4=0.
解得:${x}_{1}=\frac{10-4\sqrt{5}}{5}$,${x}_{2}=\frac{10+4\sqrt{5}}{5}$.
将x=$\frac{10-4\sqrt{5}}{5}$代入y=-$\frac{1}{2}x+5$得:y=$\frac{20+2\sqrt{5}}{5}$,
将x=$\frac{10+4\sqrt{5}}{5}$代入y=-$\frac{1}{2}x+5$得,y=$\frac{20-2\sqrt{5}}{5}$.
∴点M的坐标为($\frac{10-4\sqrt{5}}{5}$,$\frac{20+2\sqrt{5}}{5}$)或($\frac{10+4\sqrt{5}}{5}$,$\frac{20-2\sqrt{5}}{5}$).
综上所述,点M的坐标为($\frac{3}{2}$,$\frac{17}{4}$)或($\frac{-2+2\sqrt{41}}{5}$,$\frac{26-\sqrt{41}}{5}$)或($\frac{-2-2\sqrt{41}}{5}$,$\frac{26+\sqrt{41}}{5}$)或($\frac{10-4\sqrt{5}}{5}$,$\frac{20+2\sqrt{5}}{5}$)或($\frac{10+4\sqrt{5}}{5}$,$\frac{20-2\sqrt{5}}{5}$).
点评 本题主要考查的是一次函数的综合应用、矩形的性质和判定、勾股定理的应用、平行线分线段成比例定理、待定系数法求一次函数的解析式、菱形的性质、两点间的距离公式,依据两点间的距离公式列出关于x的方程是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
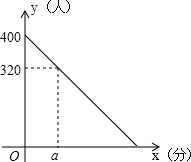 春节期间,某客运站旅客流量不断增大,旅客往往需长时间排队等候购票.经调查发现,每天开始售票时,约有400名旅客排队等候购票,同时又有新的旅客不断进入售票厅排队等候购票.售票时售票厅每分钟新增购票人数4人,每分钟每个售票窗口出售的票数3张,规定每人只购一张票.某天若同时开放两个售票窗口,售票厅排队等候购票的人数y(人)与售票时间x(分)的关系如图所示.
春节期间,某客运站旅客流量不断增大,旅客往往需长时间排队等候购票.经调查发现,每天开始售票时,约有400名旅客排队等候购票,同时又有新的旅客不断进入售票厅排队等候购票.售票时售票厅每分钟新增购票人数4人,每分钟每个售票窗口出售的票数3张,规定每人只购一张票.某天若同时开放两个售票窗口,售票厅排队等候购票的人数y(人)与售票时间x(分)的关系如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com