
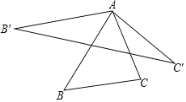
【题目】如图,将△ABC的边AB绕着点A顺时针旋转α(0°<α<90°)得到AB′,边AC绕着点A逆时针旋转β(0°<β<90°)得到AC′,连结B′C′,当α+β=60°时,我们称△AB′C’是△ABC的“蝴蝶三角形”,已知一直角边长为2的等腰直角三角形,那么它的“蝴蝶三角形”的面积为_________.
【答案】![]() +1或1
+1或1
【解析】
分两种情形分别画出图形求解即可.
如图1中,当△AB′C′是△ABC的“双展三角形”时,作C′D⊥B′A交B′A的延长线于D,在C′D上取一点F,使得FA=FC,连接AF.
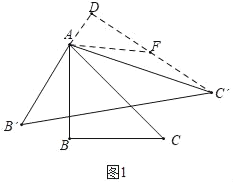
∵B∠B′AC′=60°+45°=105°,
∴∠DAC′=75°,
∵∠D=90°,
∴∠DC′A=15°,
∵FA=FC′,
∴∠FAC=∠FC′A=15°,
∴∠AFD=∠FAC+∠FC′A=30°,设AD=x,则AF=FC′=2x.DF=![]() x,
x,
∵AB=BC=2,∠B=90°,
∴AC=AC′=2![]() ,
,
在Rt△ADC′中,则有x2+(![]() x+2x)2=(2
x+2x)2=(2![]() )2,
)2,
解得x=![]() ﹣1(负根已经舍弃),
﹣1(负根已经舍弃),
∴DC′=2x+![]() x=
x=![]() +1,
+1,
∴S△AB′C′=![]() AB′C′D=
AB′C′D=![]() +1.
+1.
如图2中,当△A′BC′是△ABC的“双展三角形”时,作C′D⊥B′A交A′B的延长线于D.
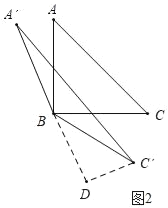
由题意:∠A′BC′=60°+90°=150°,
∴∠C′BD=30°,
∴C′D=![]() BC′=1,
BC′=1,
∴S△A′BC′=![]() BA′C′D=1,
BA′C′D=1,
综上所述,满足条件的![]() +1或1.
+1或1.
故答案为![]() +1或1.
+1或1.


科目:初中数学 来源: 题型:
【题目】现有一段120m的篱笆,准备用这些篱笆借助一段墙角围成如图所示两块面积相同的矩形场地养鸡.
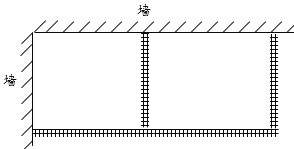
(1)如图所示,若围成的场地总面积为1750m2,则该场地的宽(图中纵向)应为多少?
(2)能不能围成面积为2000m2的场地?若能,求出此时篱笆的宽;若不能,求围成场地面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
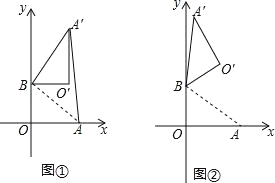
【题目】在平面直角坐标系中,O 为原点,点 A(4,0),点 B(0,3),把△ABO 绕点 B 逆时针旋转,得△A′BO′,点 A、O 旋转后的对应点为 A′、O′,记旋转角为ɑ.
(1)如图 1,若ɑ=90°,求 AA′的长;
(2)如图 2,若ɑ=120°,求点 O′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,已知点M0的坐标为(1,0),将线段O M0绕原点O沿逆时针方向旋转45°,再将其延长到M1,使得M1 M0⊥O M0,得到线段OM1;又将线段OM1绕原点O沿逆时针方向旋转45°,再将其延长到M2,使得M2M1⊥OM1,得到线段OM2,如此下去,得到线段OM3,OM4,…,OMn
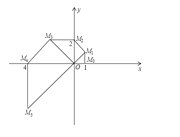
(1)写出点M5的坐标;
(2)求△M5OM6的周长;
(3)我们规定:把点Mn(xn,yn)(n=0,1,2,3…)的横坐标xn,纵坐标yn都取绝对值后得到的新坐标(|xn|,|yn|)称之为点Mn的“绝对坐标”.根据图中点Mn的分布规律,请你猜想点Mn的“绝对坐标”,并写出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D是AB上一点,DE⊥AC于点E,F是AD的中点,FG⊥BC于点G,与DE交于点H,若FG=AF,AG平分∠CAB,连接GE,GD.
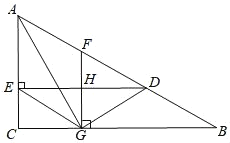
(1)求证:△ECG≌△GHD;
(2)小亮同学经过探究发现:AD=AC+EC.请你帮助小亮同学证明这一结论.
(3)若∠B=30°,判定四边形AEGF是否为菱形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小学学生较多,为了便于学生尽快就餐,师生约定:早餐一人一份,一份两样,一样一个,食堂师傅在窗口随机发放(发放的食品价格一样),食堂在某天早餐提供了猪肉包、面包、鸡蛋、油饼四样食品.
(1)按约定,“小李同学在该天早餐得到两个油饼”是 事件;(可能,必然,不可能)
(2)请用列表或树状图的方法,求出小张同学该天早餐刚好得到猪肉包和油饼的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
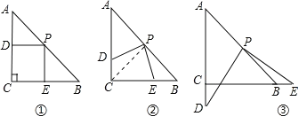
【题目】操作:在△ABC中,AC=BC=4,∠C=90°,将一块直角三角板的直角顶点放在斜边AB的中点P处,将三角板绕点P旋转,三角板的两直角边分别交射线AC、CB于D、E两点。如图①、②、③是旋转三角板得到的图形中的3种情况。
探究:
(1)如图①,PD⊥AC于D,PE⊥BC于E,则重叠部分四边形DCEP的面积为___,周长___.
(2)三角板绕点P旋转,观察线段PD与PE之间有什么数量关系?并结合图②加以证明;
(3)三角板绕点P旋转,△PBE是否能成为等腰三角形?若能,指出所有情况(即写出△PBE为等腰三角形时CE的长);若不能,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com