
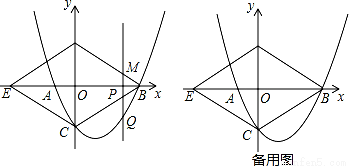
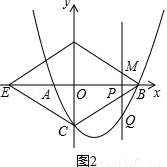
如图,已知抛物线y=ax2+bx﹣4与x轴交于A(﹣2,0),B(8,0)两点,与y轴交于点C,连接BC,以BC为一边,作菱形BDEC,使其对角线在坐标轴上,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.
(1)求抛物线的解析式;
(2)将抛物线向上平移n个单位,使其顶点在菱形BDEC内(不含菱形的边),求n的取值范围;
(3)当点P在线段OB上运动时,直线l交BD于点M.试探究m为何值时,四边形CQMD是平行四边形,并说明理由.
(1)y=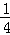 x2﹣
x2﹣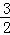 x﹣4;(2)
x﹣4;(2)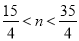 ;(3)m=4时,四边形CQMD是平行四边形,理由详见解析.
;(3)m=4时,四边形CQMD是平行四边形,理由详见解析.
【解析】
试题分析:(1)由待定系数法即可求得.
(2)先求得直线BC的解析式和抛物线的顶点坐标G(3,﹣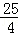 ),然后把x=3代入直线BC的解析式即可求得F的坐标,进而求得E的坐标即可求得n的取值.
),然后把x=3代入直线BC的解析式即可求得F的坐标,进而求得E的坐标即可求得n的取值.
(3)由菱形的对称性可知,点D的坐标,根据待定系数法可求直线BD的解析式,根据平行四边形的性质可得关于m的方程,求得m的值;再根据平行四边形的判定可得四边形CQBM的形状;
试题解析:(1)∵抛物线y=ax2+bx﹣4与x轴交于A(﹣2,0),B(8,0)两点,
∴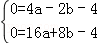 解得
解得
∴抛物线的解析式为:y=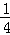 x2﹣
x2﹣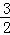 x﹣4;
x﹣4;
(2)设抛物线的顶点为G,过G点作x轴的垂线交BD于E,交BC于F,
由抛物线的解析式y=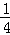 x2﹣
x2﹣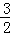 x﹣4可知C(0,﹣4)
x﹣4可知C(0,﹣4)
设直线BC的解析式为y=k1x+b1,
∵B(8,0),C(0,﹣4),则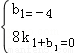 ,
,
解得k1= ,b1=﹣4.
,b1=﹣4.
故直线BC的解析式为y= x﹣4.
x﹣4.
∵y=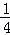 x2﹣
x2﹣ x﹣4=
x﹣4=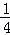 (x﹣3)2﹣
(x﹣3)2﹣ ,
,
∴抛物线的顶点G的坐标(3,﹣ ),
),
当x=3时,y= x﹣4=﹣
x﹣4=﹣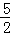 ,
,
∴F(3,﹣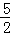 ),
),
由菱形的对称性可知,点E的坐标为(3,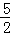 ).
).
∵GF=﹣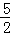 ﹣(﹣
﹣(﹣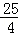 )=
)= ,GE=
,GE= ﹣(﹣
﹣(﹣ )=
)=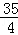 ,
,
∴ <n<
<n<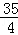 .
.
(3)∵C(0,﹣4)
∴由菱形的对称性可知,点D的坐标为(0,4).
设直线BD的解析式为y=kx+b,则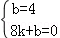 ,
,
解得k=﹣ ,b=4.
,b=4.
∴直线BD的解析式为y=﹣ x+4.
x+4.
∵l⊥x轴,
∴点M的坐标为(m,﹣ m+4),点Q的坐标为(m,
m+4),点Q的坐标为(m, m2﹣
m2﹣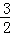 m﹣4).
m﹣4).
如图,当MQ=DC时,四边形CQMD是平行四边形,
∴(﹣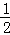 m+4)﹣(
m+4)﹣( 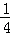 m2﹣
m2﹣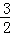 m﹣4)=4﹣(﹣4).
m﹣4)=4﹣(﹣4).
化简得:m2﹣4m=0,
解得m1=0(不合题意舍去),m2=4.
∴当m=4时,四边形CQMD是平行四边形.

考点:1.待定系数法求函数解析式;2.平行四边形判定


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源:2015届北京市顺义区八年级下学期期末考试数学试卷(解析版) 题型:选择题
下列各图形中不是中心对称图形的是( )
A.等边三角形 B.平行四边形 C.矩形 D.正方形
查看答案和解析>>
科目:初中数学 来源:2015届北京市门头沟区八年级下学期期末考试数学试卷(解析版) 题型:选择题
下列图形中,既是轴对称图形,又是中心对称图形的是( )
A.角 B.等边三角形 C.平行四边形 D.矩形
查看答案和解析>>
科目:初中数学 来源:2015届北京市昌平区八年级下学期期末考试数学试卷(解析版) 题型:解答题
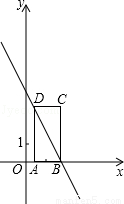
如图,在平面直角坐标系xOy中,矩形ABCD的边AD=3,A(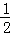 ,0),B(2,0),
,0),B(2,0),
直线y=kx+b经过B,D两点.
(1)求直线y=kx+b的解析式;
(2)将直线y=kx+b平移,若它与矩形有公共点,直接写出b的取值范围.
查看答案和解析>>
科目:初中数学 来源:2015届北京市八年级下学期期中数学试卷(解析版) 题型:解答题
如图,在平行四边形ABCD中,E、F分别在AB、CD边上,且AE=CF。
(1)求证:△ADE≌△CBF;
(2)求证:四边形BFDE是平行四边形。

查看答案和解析>>
科目:初中数学 来源:2015届北京市房山区八年级下学期期末考试数学试卷(解析版) 题型:选择题
正方形具有而矩形没有的性质是( )
A.对角线互相平分 B.对边相等
C.对角线相等 D.每条对角线平分一组对角
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com