
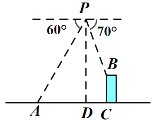
【题目】如图,无人机在600米高空的P点,测得地面A点和建筑物BC的顶端B的俯角分别为60°和70°,已知A点和建筑物BC的底端C的距离为286![]() 米,求建筑物BC的高.(结果保留整数,参考数据:
米,求建筑物BC的高.(结果保留整数,参考数据:![]() ≈1.73,sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)
≈1.73,sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)
科目:初中数学 来源: 题型:
【题目】为了美化校园,学校决定利用现有的2660盆甲种花卉和3000盆乙种花卉搭配A、B两种园艺造型共50个摆放在校园内,已知搭配一个A种造型需甲种花卉70盆,乙种花卉30盆,搭配一个B种造型需甲种花卉40盆,乙种花卉80盆.则符合要求的搭配方案有几种( )
A. 2B. 3C. 4D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 1,折叠矩形纸片 ABCD,具体操作:①点 E 为 AD 边上一点(不与点 A,D 重合),把△ABE 沿 BE 所在的直线折叠,A 点的对称点为 F 点;②过点 E 对折∠DEF,折痕EG 所在的直线交 DC 于点 G,D 点的对称点为 H 点.
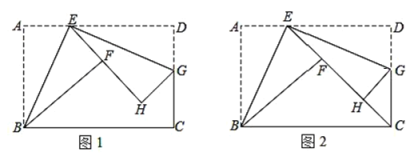
(1)求证:△ABE∽△DEG.
(2)若 AB=6,BC=10
①点 E 在移动的过程中,求 DG 的最大值;
②如图 2,若点 C 恰在直线 EF 上,连接 DH,求线段 DH 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
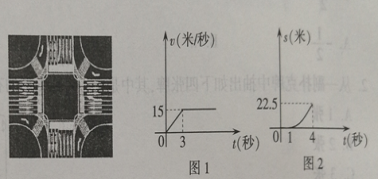
【题目】在长、宽均为![]() 米的十字路口,现遇到红灯,有
米的十字路口,现遇到红灯,有![]() 辆车依次呈一直线停在路口的交通白线后,每二辆车间隔为
辆车依次呈一直线停在路口的交通白线后,每二辆车间隔为![]() 米每辆车长
米每辆车长![]() 米.每辆车的速度
米.每辆车的速度![]() (米/秒)关于时间(秒)的函数(如图1)所示,当绿灯亮起第一辆车的车头与交通白线的距离
(米/秒)关于时间(秒)的函数(如图1)所示,当绿灯亮起第一辆车的车头与交通白线的距离![]() (米)关于时间(秒)的丽数解析式为
(米)关于时间(秒)的丽数解析式为![]() ,如图2所示.当前车启动后,后面一辆车在
,如图2所示.当前车启动后,后面一辆车在![]() 秒后也启动.
秒后也启动.
![]() 求
求![]() 的值.
的值.
![]() 当
当![]() 时,求第一辆车的车头与交通白线的距离
时,求第一辆车的车头与交通白线的距离![]() (米)关于时间(秒)的函数解析式.
(米)关于时间(秒)的函数解析式.
![]() 当
当![]() 时,求第.辆车和第一辆车在这个十字路口中的最大间距(第一辆车的车尾和第二辆车的车头哦).
时,求第.辆车和第一辆车在这个十字路口中的最大间距(第一辆车的车尾和第二辆车的车头哦).
![]() 绿灯持续时间至少要设置多长才能保证在绿灯期间这十辆车都能通过交通白线.
绿灯持续时间至少要设置多长才能保证在绿灯期间这十辆车都能通过交通白线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,“圆材埋壁”是我国古代著名的数学著作《九章算术》中的一个问题,“今有圆材,埋在壁中,不知大小,以锯锯之,深两寸,锯道长八寸,问径几何?”用现代的数学语言表述是:“![]() 为
为![]() 的直径,弦
的直径,弦![]() ,垂足为点
,垂足为点![]() ,
,![]() 寸,
寸,![]() 寸,求直径
寸,求直径![]() 的长?”依题意
的长?”依题意![]() 的长为( )
的长为( )
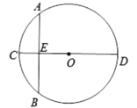
A.6寸B.8寸C.10寸D.12寸
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】酒令是中国民间风俗之一.白居易曾诗曰:“花时同醉破春愁,醉折花枝当酒筹”饮酒行令,是中国人在饮酒时助兴的一种特有方式,不仅要以酒助兴,往往还伴之以赋诗填词、猜迷形拳之举,最早诞生于西周,完备于隋唐,“虎棒鸡虫令”是其中一种:“二人相对,以筷子相声,同时或喊虎、喊棒、喊鸡、喊虫,以棒打虎、虎吃鸡、鸡吃虫、虫嗑棒论胜负,负者饮.若棒兴鸡、或虫兴虎同时出现(解释:若棒与鸡,虎与虫同时喊出)或两人喊出同一物,则不分胜负,继续喊”.依据上述规则,张三和李四同时随机地喊出其中一物,两人只喊一次.
(1)求张三喊出“虎”取胜的概率;
(2)用列表法或画树状图法,求李四取胜的概率;
(3)直接写出两人能分出胜负的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是射线
是射线![]() 上的动点,连接
上的动点,连接![]() ,将
,将![]() 沿着
沿着![]() 翻折得到
翻折得到![]() ,设
,设![]()
![]() ,
,

(1)如图1,当点![]() 在
在![]() 上时,求
上时,求![]() 的值.
的值.
(2)如图2,连接![]() ,
,![]() ,当
,当![]() 时,求
时,求![]() 的面积.
的面积.
(3)在点![]() 的运动过程中,当
的运动过程中,当![]() 是等腰三角形时,求
是等腰三角形时,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com