
 如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y=$\frac{{m}^{2}+2m-9}{x}$的图象上,若点A的坐标为(-2,3),则m的值为( )
如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y=$\frac{{m}^{2}+2m-9}{x}$的图象上,若点A的坐标为(-2,3),则m的值为( )| A. | 1 | B. | 3 | C. | 3或-5 | D. | 1或-3 |
分析 根据矩形的对角线将矩形分成面积相等的两个直角三角形,找到图中的所有矩形及相等的三角形,即可推出S四边形CEOF=S四边形HAGO,根据反比例函数比例系数的几何意义即可求出m2+2m-9=-6,再解出m的值即可.
解答 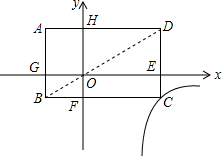 解:如图:
解:如图:
∵四边形ABCD、GBFO、CEOF、OEDH为矩形,
又∵BO为四边形GBFO的对角线,OD为四边形OEDH的对角线,
∴S△BOG=S△BOF,S△OHD=S△OED,S△ABD=S△CDB,
∴S△ABD-S△BOG-S△HOD=S△BCD-S△BOF-S△OED,
∴S四边形AGOH=S四边形CEOF=2×3=6,
∴xy=m2+2m-9=-6,
解得m=1或m=-3.
故选D.
点评 本题考查了反比例函数k的几何意义、矩形的性质、一元二次方程的解法,关键是判断出S四边形CEOF=S四边形HAGO.


科目:初中数学 来源: 题型:选择题
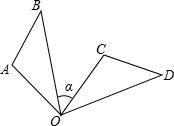 如图,△OAB绕点O顺时针旋转85°到△OCD,已知∠A=110°,若∠D=40°,则∠α的度数是( )
如图,△OAB绕点O顺时针旋转85°到△OCD,已知∠A=110°,若∠D=40°,则∠α的度数是( )| A. | 30° | B. | 45° | C. | 55° | D. | 60° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com