
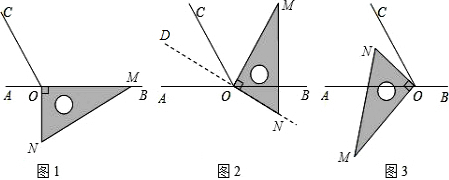
分析 (1)利用角平分线的定义结合直角三角板的内角度数即可分别判断得出答案;
(2)首先根据∠COM=120°-∠BOM,∠BON=90°-∠BOM,进而得出答案;
(3)因为∠MON=90°,∠AOC=60°,所以∠AOM=90°-∠AON,∠NOC=60°-∠AON,然后作差即可.
解答 解:(1)∵∠BOC=120°,OM平分∠BOC,
∴∠BOM=60°,故①正确;
∵∠BOM=60°,∠MON=90°,
∴∠COM=60°,∠BON=30°,
∴∠COM-∠BON=30°,故②正确;
∵∠BOM=60°,∠BON=30°,
∴OB平分∠MON,错误;
∵∠BOC=120°,∠BON=30°,
∴∠AOD=∠COD=30°,
∴∠AOC的平分线在直线ON上,故④正确;
故答案为:①②④;
(2)①∵∠COM=120°-∠BOM,
∠BON=90°-∠BOM,
∴∠COM-∠BON=120°-90°=30°;
②由题意可得:∠COM+∠BON=120°-90°=30°;
(3)∵∠AOM=90°-∠AON,∠CON=∠AOC-∠AON=60°-∠AON,
∴∠AOM-∠CON=90°-60°=30°.
点评 此题考查了角平分线的定义,应该认真审题并仔细观察图形,找到各个量之间的关系,是解题的关键.


科目:初中数学 来源: 题型:解答题
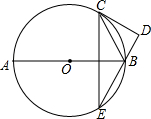 如图,AB为⊙O的直径,C为⊙O上一点,CD切⊙O于点C,BD⊥CD,BD交⊙O于点E,连CE.
如图,AB为⊙O的直径,C为⊙O上一点,CD切⊙O于点C,BD⊥CD,BD交⊙O于点E,连CE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
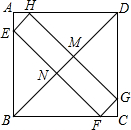 如图,四边形EFGH的四个顶点E、F、G、H分别在正方形ABCD的AB、BC、CD、DA上滑动,在滑动的过程中,始终有EH∥BD∥FG,且EH=FG,四边形EFGH的周长为$2\sqrt{2}a$,那么正方形ABCD的周长为4a.
如图,四边形EFGH的四个顶点E、F、G、H分别在正方形ABCD的AB、BC、CD、DA上滑动,在滑动的过程中,始终有EH∥BD∥FG,且EH=FG,四边形EFGH的周长为$2\sqrt{2}a$,那么正方形ABCD的周长为4a.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
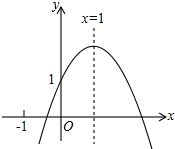 二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,有如下结论:①c<1;②2a+b=0;③已知点A(x1,y1),B(x2,y2)在该抛物线上,当x1>x2,则y1>y2;④若方程ax2+bx+c=0有两个根,其中一个根为3,则另一个根为-1,则正确的结论是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,有如下结论:①c<1;②2a+b=0;③已知点A(x1,y1),B(x2,y2)在该抛物线上,当x1>x2,则y1>y2;④若方程ax2+bx+c=0有两个根,其中一个根为3,则另一个根为-1,则正确的结论是( )| A. | ①② | B. | ①③ | C. | ②④ | D. | ③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -(+8)=8 | B. | -(-3)=-3 | C. | -$\frac{2}{3}$<-$\frac{1}{2}$ | D. | -π>-3.14 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
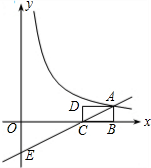 如图,矩形ABCD中,AB=1,BC=2,BC在x轴上,一次函数y=kx-2的图象经过点A、C,并与y轴交于点E,反比例函数y=$\frac{m}{x}$的图象经过点A.
如图,矩形ABCD中,AB=1,BC=2,BC在x轴上,一次函数y=kx-2的图象经过点A、C,并与y轴交于点E,反比例函数y=$\frac{m}{x}$的图象经过点A.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 某校为了解学生喜爱的体育活动项目,随机抽查了100名学生,让每人选一项自己喜欢的项目,并制成如图所示的扇形统计图.如果该校有600名学生,则喜爱跳绳的学生约有180人.
某校为了解学生喜爱的体育活动项目,随机抽查了100名学生,让每人选一项自己喜欢的项目,并制成如图所示的扇形统计图.如果该校有600名学生,则喜爱跳绳的学生约有180人.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com