
 如图,已知抛物线与x轴交于点A(2,0),B(-4,0),与y轴交于C(0,8).
如图,已知抛物线与x轴交于点A(2,0),B(-4,0),与y轴交于C(0,8).分析 (1)设交点式y=a(x+4)(x-2),然后把C点坐标代入求出a的值即可得到抛物线解析式为,再把解析式配成顶点式即可得到顶点D的坐标;
(2)设P(-2,t),利用待定系数法求出直线CD的解析式为y=-x+8,则可得到E点和Q点坐标,于是可△OCE为等腰直角三角形得到∠OCE=45°,接着判断△PQM为等腰直角三角形得到PQ=$\sqrt{2}$PM,然后利用PQ=|10-t|,PM=PO=$\sqrt{{2}^{2}+{t}^{2}}$建立方程|10-t|=$\sqrt{2}$•$\sqrt{4+{t}^{2}}$解方程求出t即可得到P点坐标;
(3)先确定F(-4,12),设平移后的抛物线解析式为y=-x2-2x+8+m,当方程-x2-2x+8+m=-x+8有相等实数解时,平移后的抛物线与线段EF只有一个公共点,则利用判别式判别式的意义可解出m=-$\frac{1}{4}$,再分别计算平移的抛物线过点E和F所对应的m的值,然后根据抛物线的几何变换可判断抛物线向上最多可平移的单位长度和向下最多可平移的单位长度.
解答 解:(1)设抛物线解析式为y=a(x+4)(x-2),
把C(0,8)代入得a•4•(-2)=8,解得a=-1,
所以抛物线解析式为y=-(x+4)(x-2),即y=-x2-2x+8,
因为y=-(x+1)2+9,
所以顶点D的坐标为(-1,9);
(2)存在.
线段OB的垂直平分线为直线x=-2,设P(-2,t),
设直线CD的解析式为y=kx+b,
把C(0,8),D(-1,9)代入得$\left\{\begin{array}{l}{b=8}\\{-k+b=9}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-1}\\{b=8}\end{array}\right.$,
所以直线CD的解析式为y=-x+8,
当x=-2时,y=-x+8=10,则Q(-2,10),
当y=0时,-x+8=0,解得x=8,则E(8,0),
∴△OCE为等腰直角三角形,
∴∠OCE=45°,
∵PQ∥OC,
∴∠PQE=∠OCE=45°,
而PM⊥CD于M.
∴△PQM为等腰直角三角形,
∴PQ=$\sqrt{2}$PM,
∵PQ=|10-t|,PM=PO=$\sqrt{{2}^{2}+{t}^{2}}$,
∴|10-t|=$\sqrt{2}$•$\sqrt{4+{t}^{2}}$,
整理得t2+20t-92=0,解得t1=-10+8$\sqrt{3}$,t2=-10-8$\sqrt{3}$,
∴满足条件的P点坐标为(-2,-10+8$\sqrt{3}$)或(-2,-10-8$\sqrt{3}$);
(3)当x=-4时,y=-x+8=12,则F(-4,12),
设平移后的抛物线解析式为y=-x2-2x+8+m,
当方程-x2-2x+8+m=-x+8,即x2+x-m=0有相等实数解时,平移后的抛物线与线段EF只有一个公共点,所以△=12-4(-m)=0,解得m=-$\frac{1}{4}$;
当抛物线过点E(8,0)时,-64-16+8+m=0,解得m=72,
当抛物线过点F(-4,12)时,-16+8+8+m=12,解得m=12,
所以抛物线向上最多可平移72个单位长度,向下最多可平移$\frac{1}{4}$个单位长度.
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、一次函数图象上点的坐标特征和二次函数的性质;会利用待定系数法求函数解析式;理解坐标与图形性质;灵活应用等腰直角三角形的性质进行几何计算;利用抛物线的几何变换.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,在矩形ABCD中.AB=3,BC=4,沿EF折叠,折痕为EF,使C点落到A点处,点D落到G处.
如图,在矩形ABCD中.AB=3,BC=4,沿EF折叠,折痕为EF,使C点落到A点处,点D落到G处.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
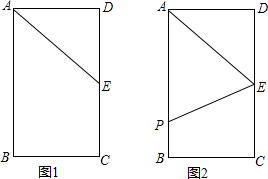
 如图,在等腰△ABC中,AB=BC=4,点O是AB的中点,∠AOC=60°,点P是射线CO上的一个动点,若当△PAB为直角三角线时,试画出可能的图形(两种即可),并求出相应图形中的AP的长.
如图,在等腰△ABC中,AB=BC=4,点O是AB的中点,∠AOC=60°,点P是射线CO上的一个动点,若当△PAB为直角三角线时,试画出可能的图形(两种即可),并求出相应图形中的AP的长.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.5×106 | B. | 1.5×107 | C. | 1.5×108 | D. | 1.5×109 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图:在△ABE中,点C是BE边上的一点,连接AC,已知AD是∠BAC的角平分线,EF是AD的垂直平分线且交AB边于点F.
如图:在△ABE中,点C是BE边上的一点,连接AC,已知AD是∠BAC的角平分线,EF是AD的垂直平分线且交AB边于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
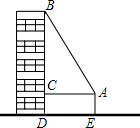 如图,一高层住宅发生火灾,消防车立即赶到距大厦5米处(车尾AE到大厦墙面CD的距离为5米),升起云梯到火灾窗口B,已知云梯AB长13米,云梯底部距地面的高AE为3米,求发生火灾的住户窗口距地面的高BD是多少米?
如图,一高层住宅发生火灾,消防车立即赶到距大厦5米处(车尾AE到大厦墙面CD的距离为5米),升起云梯到火灾窗口B,已知云梯AB长13米,云梯底部距地面的高AE为3米,求发生火灾的住户窗口距地面的高BD是多少米?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com