
 如图,菱形ABCD中,分别延长DC,BC至点E,F,使CE=CD,CF=CB,联结DB,BE,EF,FD.
如图,菱形ABCD中,分别延长DC,BC至点E,F,使CE=CD,CF=CB,联结DB,BE,EF,FD.分析 (1)根据菱形的性质得出CE=CD,CF=CB,再根据矩形的判定证明即可.
(2)根据菱形的面积等于对角线乘积的一半,得出DB的长度,再根据含30°直角三角形的性质解答即可.
解答 (1)证明:∵CE=CD,CF=CB,
∴四边形DBEF是平行四边形.
∵四边形ABCD是菱形,
∴CD=CB.
∴CE=CF,
∴BF=DE,
∴四边形DBEF是矩形.
(2)设DB为2a,
∵∠A=60°,菱形ABCD的面积为$8\sqrt{3}$,
∴可得$\frac{1}{2}•2a•2\sqrt{3}a=8\sqrt{3}$,
解得:a=2,
∴DB=4,
∵∠DBC=60°,
∴DF=$4\sqrt{3}$.
点评 此题考查菱形的性质,关键是根据菱形的性质和矩形的判定解答,同时根据菱形的面积和直角三角形的性质分析.


科目:初中数学 来源: 题型:选择题
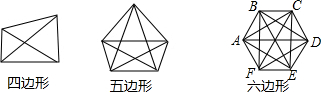
| A. | 12,20 | B. | 12,15 | C. | 9,10 | D. | 9,12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
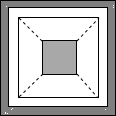 如图所示,2013个圆由小到大套在一起,从外向里相间画上阴影,最外面一层画阴影,最里面一层画阴影,最外面的正方形的边长为2013cm,向里依次为2012cm,2011cm,…,1cm,那么在这个图形中,所有画阴影部分的面积和是多少?(结果保留π)
如图所示,2013个圆由小到大套在一起,从外向里相间画上阴影,最外面一层画阴影,最里面一层画阴影,最外面的正方形的边长为2013cm,向里依次为2012cm,2011cm,…,1cm,那么在这个图形中,所有画阴影部分的面积和是多少?(结果保留π)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
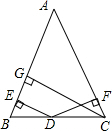 如图所示,已知在△ABC中,AB=AC,CG⊥AB,点D是BC边上的一点,DE⊥AB,DF⊥AC.
如图所示,已知在△ABC中,AB=AC,CG⊥AB,点D是BC边上的一点,DE⊥AB,DF⊥AC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com