Question

9．某中学以“我最喜爱的书籍”为主题，对学生最喜爱的书籍类型进行随机抽样调查，收集整理数据后，给出如下两幅未完成的统计图，请根据图①和图②所提供的信息，解答下列问题：

（1）填空：在这次抽样查中，一共调查了300名学生；
（2）把折线统计图①补充完整；
（3）求出扇形统计图②中体育部分所对应的圆心角的度数；
（4）如果这所中学共有学生1800名，那么你估计最喜爱科普类书籍的学生人数．

Answer 1

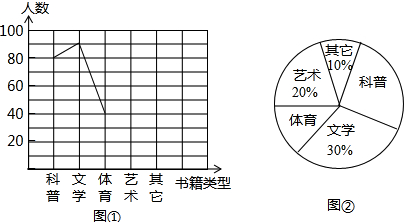
分析 （1）用文学的人数除以所占的百分比计算即可得解；
（2）根据所占的百分比求出艺术和其它的人数，然后补全折线图即可；
（3）用体育所占的百分比乘以360°，计算即可得解；
（4）用总人数乘以科普所占的百分比，计算即可得解．

解答 解：（1）90÷30%=300（名），
故一共调查了300名学生；
故答案为：300；

（2）艺术的人数：300×20%=60名，
其它的人数：300×10%=30名；
补全折线图如图：
；

（3）体育部分所对应的圆心角的度数为：$\frac{40}{300}$×360°=48°；

（4）1800×$\frac{80}{300}$=480（名）．
答：1800名学生中估计最喜爱科普类书籍的学生人数为480人．

点评 本题考查的是折线统计图和扇形统计图的综合运用，折线统计图表示的是事物的变化情况，扇形统计图中每部分占总部分的百分比等于该部分所对应的扇形圆心角的度数与360°的比．