
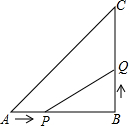
 如图,在△ABC中,∠B=90°,AB=6cm,BC=6cm,点P从点A出发沿AB边向点B以1cm/秒的速度移动,点Q从点B出发沿BC边向点C以2cm/秒的速度移动.
如图,在△ABC中,∠B=90°,AB=6cm,BC=6cm,点P从点A出发沿AB边向点B以1cm/秒的速度移动,点Q从点B出发沿BC边向点C以2cm/秒的速度移动.分析 (1)由题意,可设P、Q经过t秒,使△PBQ的面积为8cm2,则PB=6-t,BQ=2t,根据三角形面积的计算公式,S△PBQ=$\frac{1}{2}$BP×BQ,列出表达式,解答出即可;
(2)把S△PBQ=8代入求得相应的t的值即可;
(3)可设P、Q两点运动t秒时,PQ有最小值,则PB=6-t,BQ=2t,根据勾股定理,可得PQ2=BP2+BQ2,代入整理即可求出其最小值;
解答 解:(1)设P、Q经过t秒时,△PBQ的面积为8cm2,
则PB=6-t,BQ=2t,
∵∠B=90°,
∴S△PBQ=$\frac{1}{2}$BP×BQ=$\frac{1}{2}$(6-t)×2t=-t2+6t,即S=-t2+6t(0≤t≤6);
(2)由(1)得到S=-t2+6t.
当S=8时,-t2+6t=8,
解得,t1=2,t2=4,
∴当P、Q经过2或4秒时,△PBQ的面积为8cm2;
(2)设P、Q两点运动t秒时,PQ有最小值,
∴PQ2=(6-t)2+(2t)2,
整理得,PQ2=5(t-$\frac{6}{5}$)2+$\frac{144}{5}$,
∴当t=$\frac{6}{5}$时,PQ有最小值为:$\frac{12\sqrt{5}}{5}$.
点评 本题主要考查了一元二次方程的应用和二次函数及其最值,根据题意,正确表示出边长及配方法求出最值,是解答本题的关键.


科目:初中数学 来源: 题型:填空题
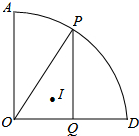 如图,扇形AOD中,∠AOD=90°,OA=8,点P为弧AD上一动点,PQ⊥OD于点Q,点I为△OPQ的内心,当点P从点A沿弧AD运动到点D时,点I运动的路径长为2$\sqrt{2}π$.
如图,扇形AOD中,∠AOD=90°,OA=8,点P为弧AD上一动点,PQ⊥OD于点Q,点I为△OPQ的内心,当点P从点A沿弧AD运动到点D时,点I运动的路径长为2$\sqrt{2}π$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 打高尔夫球时,球的飞行路线可以看成是一条抛物线,如果不考虑空气的阻力,某次球的飞行高度y(单位:米)与飞行距离x(单位:百米)满足二次函数:y=-5x2+20x,这个球飞行的水平距离最远是多少米?球的飞行高度能否达到40m?
打高尔夫球时,球的飞行路线可以看成是一条抛物线,如果不考虑空气的阻力,某次球的飞行高度y(单位:米)与飞行距离x(单位:百米)满足二次函数:y=-5x2+20x,这个球飞行的水平距离最远是多少米?球的飞行高度能否达到40m?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com