
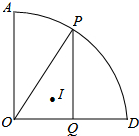
 如图,扇形AOD中,∠AOD=90°,OA=8,点P为弧AD上一动点,PQ⊥OD于点Q,点I为△OPQ的内心,当点P从点A沿弧AD运动到点D时,点I运动的路径长为2$\sqrt{2}π$.
如图,扇形AOD中,∠AOD=90°,OA=8,点P为弧AD上一动点,PQ⊥OD于点Q,点I为△OPQ的内心,当点P从点A沿弧AD运动到点D时,点I运动的路径长为2$\sqrt{2}π$. 分析 连OI,PI,DI,由△OPH的内心为I,可得到∠PIO=180°-∠IPO-∠IOP=180°-$\frac{1}{2}$(∠HOP+∠OPH)=135°,并且易证△OPI≌△ODI,得到∠DIO=∠PIO=135°,所以点I在以OD为弦,并且所对的圆周角为135°的一段劣弧上;过D、I、O三点作⊙O′,如图,连O′D,O′O,在优弧AO取点P′,连P′D,P′O,可得∠DP′O=180°-135°=45°,得∠DO′O=90°,O′O=4$\sqrt{2}$,然后求得∠OO′D=90°,从而可求得点I运动路径的长度.
解答 解:如图,连OI,PI,DI,过D、I、O三点作⊙O′,连O′D、O′O,在优弧DO取点P′,连P′D,P′O.
.
∵△OPH的内心为I,
∴∠IOP=∠IOD,∠IPO=∠IPH.
∴∠PIO=180°-∠IPO-∠IOP=180°-$\frac{1}{2}$(∠HOP+∠OPH).
∵PH⊥OD,
∴∠PHO=90°.
∴∠PIO=180°-$\frac{1}{2}$(∠HOP+∠OPH)=180°-$\frac{1}{2}$(180°-90°)=135°.
在△OPI和△ODI中$\left\{\begin{array}{l}{IO=IO}\\{∠POI=∠DPI}\\{OD=OP}\end{array}\right.$,
∴△OPI≌△ODI(SAS).
∴∠DIO=∠PIO=135°.
∴点I在以OD为弦,并且所对的圆周角为135°的一段劣弧上.
∵∠DIO=135°,
∴∠DP′O=180°-135°=45°.
∴∠DO′O=90°,
∵OD=8,
∴OO′=DO′=4$\sqrt{2}$.
∴劣弧OD=$\frac{1}{4}×2π×4\sqrt{2}$=2$\sqrt{2}$π.
∴点I运动的路径长为2$\sqrt{2}π$.
故答案为:2$\sqrt{2}π$.
点评 本题考查的是三角形的内切圆与内心,根据题意作出辅助线,构造出全等三角形,得出点I在以OD为弦,并且所对的圆周角为135°的一段劣弧上是解答此题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
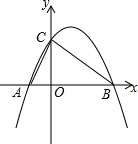 已知抛物线y=-$\frac{1}{2}$x2+(m+$\frac{1}{2}$)x+m+1与x轴交A、B两点,其中A在原点的左边,B在原点的右边(如图),与y轴交与点C.
已知抛物线y=-$\frac{1}{2}$x2+(m+$\frac{1}{2}$)x+m+1与x轴交A、B两点,其中A在原点的左边,B在原点的右边(如图),与y轴交与点C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m≠-$\frac{3}{2}$,n≠2 | B. | m≠-$\frac{3}{2}$,n=2 | C. | m=-$\frac{3}{2}$,n≠2 | D. | m=-$\frac{3}{2}$,n=2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
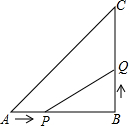 如图,在△ABC中,∠B=90°,AB=6cm,BC=6cm,点P从点A出发沿AB边向点B以1cm/秒的速度移动,点Q从点B出发沿BC边向点C以2cm/秒的速度移动.
如图,在△ABC中,∠B=90°,AB=6cm,BC=6cm,点P从点A出发沿AB边向点B以1cm/秒的速度移动,点Q从点B出发沿BC边向点C以2cm/秒的速度移动.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com