
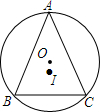
 如图,△ABC中,AB=AC=13,BC=10,⊙O为△ABC外接圆,I为△ABC的内心.
如图,△ABC中,AB=AC=13,BC=10,⊙O为△ABC外接圆,I为△ABC的内心.分析 (1)连接AO,且延长AO交BC于D,连接OB、OC,求出AD⊥BC,BD=DC,根据勾股定理求出AD,在Rt△OBD中,由勾股定理得出OB2=OD2+BD2,代入求出即可;
(2)作△ABC的内切圆I,过点I作ID⊥BC,垂足为D.先利用面积法求得ID=$\frac{10}{3}$,然后再Rt△BDI中依据勾股定理求得IB的长即可.
解答 解:(1)如图1所示:连接AO,且延长AO交BC于D,连接OB、OC.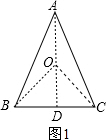
∵AB=AC,O为△ABC外接圆的圆心,
∴AD⊥BC,BD=DC,
BD=DC=$\frac{1}{2}$BC=5,
设等腰△ABC外接圆的半径为R,
则OA=OB=OC=R,
在Rt△ABD中,由勾股定理得:AD=12,
在Rt△OBD中,由勾股定理得:OB2=OD2+BD2,即R2=(12-R)2+52,
解得:R=$\frac{169}{24}$,
∴BO=$\frac{169}{24}$;
(2)如图2所示:作△ABC的内切圆I,过点I作ID⊥BC,垂足为D.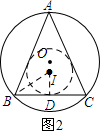
设圆I的半径为r,根据题意得$\frac{1}{2}BC•AD=\frac{1}{2}(AB+BC+AC)•r$,即$\frac{1}{2}×10×12=\frac{1}{2}×36×r$.
解得:r=$\frac{10}{3}$.
∵BC是圆I的切线,
∴ID⊥BC.
在Rt△BID中,由勾股定理得:BI=$\sqrt{I{D}^{2}+D{B}^{2}}$=$\sqrt{(\frac{10}{3})^{2}+{5}^{2}}$=$\frac{5\sqrt{13}}{3}$.
点评 本题主要考查的是三角形的内心和外心、勾股定理掌握本题的辅助线的作法是解题的关键.


科目:初中数学 来源: 题型:填空题
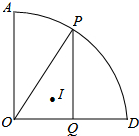 如图,扇形AOD中,∠AOD=90°,OA=8,点P为弧AD上一动点,PQ⊥OD于点Q,点I为△OPQ的内心,当点P从点A沿弧AD运动到点D时,点I运动的路径长为2$\sqrt{2}π$.
如图,扇形AOD中,∠AOD=90°,OA=8,点P为弧AD上一动点,PQ⊥OD于点Q,点I为△OPQ的内心,当点P从点A沿弧AD运动到点D时,点I运动的路径长为2$\sqrt{2}π$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 打高尔夫球时,球的飞行路线可以看成是一条抛物线,如果不考虑空气的阻力,某次球的飞行高度y(单位:米)与飞行距离x(单位:百米)满足二次函数:y=-5x2+20x,这个球飞行的水平距离最远是多少米?球的飞行高度能否达到40m?
打高尔夫球时,球的飞行路线可以看成是一条抛物线,如果不考虑空气的阻力,某次球的飞行高度y(单位:米)与飞行距离x(单位:百米)满足二次函数:y=-5x2+20x,这个球飞行的水平距离最远是多少米?球的飞行高度能否达到40m?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.212km | B. | 2.12km | C. | 21.2km | D. | 212km |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
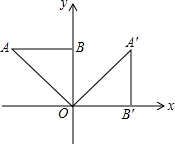 等腰直角三角形AOB的顶点A在第二象限,∠ABO=90°,点B的坐标是(0,1).若将△AOB绕点O顺时针旋转90°得到△A′OB′,则点A的对应点A′的坐标是(1,1).
等腰直角三角形AOB的顶点A在第二象限,∠ABO=90°,点B的坐标是(0,1).若将△AOB绕点O顺时针旋转90°得到△A′OB′,则点A的对应点A′的坐标是(1,1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com