
 打高尔夫球时,球的飞行路线可以看成是一条抛物线,如果不考虑空气的阻力,某次球的飞行高度y(单位:米)与飞行距离x(单位:百米)满足二次函数:y=-5x2+20x,这个球飞行的水平距离最远是多少米?球的飞行高度能否达到40m?
打高尔夫球时,球的飞行路线可以看成是一条抛物线,如果不考虑空气的阻力,某次球的飞行高度y(单位:米)与飞行距离x(单位:百米)满足二次函数:y=-5x2+20x,这个球飞行的水平距离最远是多少米?球的飞行高度能否达到40m?  直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案 培优三好生系列答案
培优三好生系列答案科目:初中数学 来源: 题型:解答题
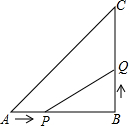 如图,在△ABC中,∠B=90°,AB=6cm,BC=6cm,点P从点A出发沿AB边向点B以1cm/秒的速度移动,点Q从点B出发沿BC边向点C以2cm/秒的速度移动.
如图,在△ABC中,∠B=90°,AB=6cm,BC=6cm,点P从点A出发沿AB边向点B以1cm/秒的速度移动,点Q从点B出发沿BC边向点C以2cm/秒的速度移动.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
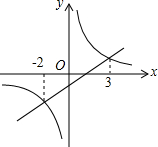 如图,一次函数y1=kx+b图象与反比例函数y2=$\frac{m}{x}$图象的两交点横坐标分别为-2、3,观察图象,写出y1>y2时,x的取值范围是-2<x<0,或x>3.
如图,一次函数y1=kx+b图象与反比例函数y2=$\frac{m}{x}$图象的两交点横坐标分别为-2、3,观察图象,写出y1>y2时,x的取值范围是-2<x<0,或x>3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
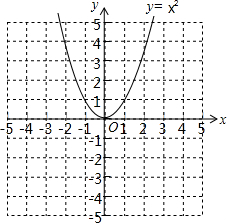 二次函数y=x2的图象如图,请将此图象向右平移1个单位,再向下平移4个单位.
二次函数y=x2的图象如图,请将此图象向右平移1个单位,再向下平移4个单位.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AD∥BE∥CF,直线l1、l2与这三条平行线分别交于点A、B、C和点D、E、F.若AB=4.5,BC=3,EF=2,则DE的长度是( )
如图,AD∥BE∥CF,直线l1、l2与这三条平行线分别交于点A、B、C和点D、E、F.若AB=4.5,BC=3,EF=2,则DE的长度是( )| A. | $\frac{4}{3}$ | B. | 3 | C. | 5 | D. | $\frac{27}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com