
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,O为直线AB上一点,OD平分∠AOC,OE平分∠COB,
如图,O为直线AB上一点,OD平分∠AOC,OE平分∠COB,查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
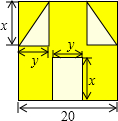 “囧”像一个人脸郁闷的神情.如图,边长为a的正方形纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分),设剪去的两个小直角三角形的两直角边长分别为x、y,剪去的小长方形长和宽也分别为x,y.
“囧”像一个人脸郁闷的神情.如图,边长为a的正方形纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分),设剪去的两个小直角三角形的两直角边长分别为x、y,剪去的小长方形长和宽也分别为x,y.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,OE为∠AOD的平分线,∠COD=$\frac{1}{4}$∠EOC,∠COD=15°,求∠AOD的大小.
如图,OE为∠AOD的平分线,∠COD=$\frac{1}{4}$∠EOC,∠COD=15°,求∠AOD的大小.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ACE中,CA=CE,∠CAE=30°,∠CAE=30°,⊙O经过点C,且圆的直径AB在线段AE上.
如图,在△ACE中,CA=CE,∠CAE=30°,∠CAE=30°,⊙O经过点C,且圆的直径AB在线段AE上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com