【题目】已知抛物线y＝ax2+bx+c经过点A（﹣3，0），B（1，0），C（0，3），求该抛物线的解析式并写出它的对称轴和顶点坐标．
长江作业本同步练习册系列答案科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系xOy中，直线y=kx+2与x轴、y轴分别交于点A(-1,0)和点B，与反比例函数y=
的图象在第一象限内交于点C（1，n）．
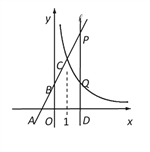
（1）求k的值；
（2）求反比例函数的解析式；
（3）过x轴上的点D（a，0）作平行于y轴的直线
（a＞1），分别与直线AB和双曲线
交于点P、Q，且PQ=2QD，求点D的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
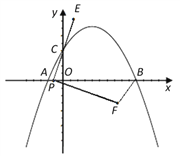
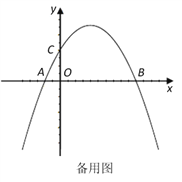
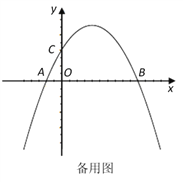
【题目】如图，在平面直角坐标系中，已知点A、B、C的坐标分别为(-1，0)，(5，0)，(0，2)．
（1）求过A、B、C三点的抛物线解析式；
（2）若点P从A点出发，沿x轴正方向以每秒1个单位长度的速度向B点移动，连接PC并延长到点E，使CE=PC，将线段PE绕点P顺时针旋转90°得到线段PF，连接FB．若点P运动的时间为t秒(0≤t≤6)，设△PBF的面积为S；
①求S与t的函数关系式；
②当t是多少时，△PBF的面积最大，最大面积是多少？
（3）点P在移动的过程中，△PBF能否成为直角三角形？若能，直接写出点F的坐标；若不能，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】反比例函数y=
的图象如图所示，以下结论：
①常数m＜﹣1；
②在每个象限内，y随x的增大而增大；
③若点A（﹣1，h），B（2，k）在图象上，则h＜k；
④若点P（x，y）在上，则点P′（﹣x，﹣y）也在图象．
其中正确结论的个数是（ ）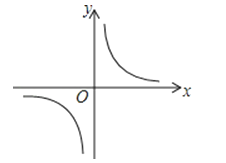
A.1
B.2
C.3
D.4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知在同一内有三点
、
、
，请你根据下列要求用直尺和圆规作图：
①画线段
， 
．
②作射线
，并在射线
上取一点
，使
．
③作射线
，并在射线
上取一点
，使
．
请根据以上作图，解答下列问题：
（
）请问
、
分别是哪两条线段的中点？并说理由．
（
）若巳知线段
的长为
，求线段
的长度．
查看答案和解析>>
科目：初中数学 来源： 题型：
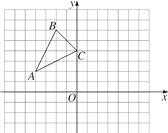
【题目】如图，已知A(－4，2)，B(－2，6)，C(0，4)是直角坐标系中的三点．
(1)把△ABC向右平移4个单位再向下平移1个单位，得到△A1B1C1，画出平移后的图形，并写出点A的对应点A1的坐标；
(2)以原点O为位似中心，将△ABC缩小为原来的一半，得到△A2B2C2，请在所给的坐标系中作出所有满足条件的图形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知反比例函数y=
（m为常数）的图象在一，三象限．
（1）求m的取值范围；
（2）如图，若该反比例函数的图象经过ABOD的顶点D，点A、B的坐标分别为（0，4），（﹣3，0）．
①求出函数解析式；
②设点P是该反比例函数图象上的一点，若OD=OP，则P点的坐标为多少？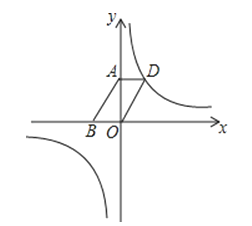
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（12分）为举办校园文化艺术节，甲、乙两班准备给合唱同学购买演出服装（一人一套），两班共92人（其中甲班比乙班人多，且甲班不到90人），下面是供货商给出的演出服装的价格表：
如果两班单独给每位同学购买一套服装，那么一共应付5020元．
（1）甲、乙两班联合起来给每位同学购买一套服装，比单独购买可以节省多少钱？
（2）甲、乙两班各有多少名同学？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
