
 如图,△ABC中,∠C=90°,三边长分别为a,b,c,⊙O与△ABC的三边均相切,求⊙O的半径r.
如图,△ABC中,∠C=90°,三边长分别为a,b,c,⊙O与△ABC的三边均相切,求⊙O的半径r. 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
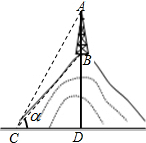 如图,在铅直高度为200m的小山上建有一座电视转播塔,某数学兴趣小组为测量电视转播塔的高度,在山脚的C处测得山顶B的仰角为30°(即∠BCD=30°),测得塔顶的仰角为45°(即∠ACD=45°),请根据以上数据求塔高AB.(精确到1m.备用数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732).
如图,在铅直高度为200m的小山上建有一座电视转播塔,某数学兴趣小组为测量电视转播塔的高度,在山脚的C处测得山顶B的仰角为30°(即∠BCD=30°),测得塔顶的仰角为45°(即∠ACD=45°),请根据以上数据求塔高AB.(精确到1m.备用数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知△ABC和过点O的两条互相垂直的直线x、y,画出△ABC关于直线x对称的△A′B′C′,再画出△A′B′C′关于直线y对称的△A″B″C″,观察△ABC与△A″B″C″,这两个三角形具有怎样的对称性?
如图,已知△ABC和过点O的两条互相垂直的直线x、y,画出△ABC关于直线x对称的△A′B′C′,再画出△A′B′C′关于直线y对称的△A″B″C″,观察△ABC与△A″B″C″,这两个三角形具有怎样的对称性?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某服装专卖店老板对第一季度男、女服装的销售收入进行统计,并绘制了扇形统计图(如图).由于三月份展开促销活动,男女服装的销售收入分别比二月份增长了40%,64%,已知第一季度男女服装的销售总收入为20万元.
某服装专卖店老板对第一季度男、女服装的销售收入进行统计,并绘制了扇形统计图(如图).由于三月份展开促销活动,男女服装的销售收入分别比二月份增长了40%,64%,已知第一季度男女服装的销售总收入为20万元.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com