
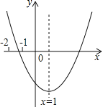
【题目】已知二次函数![]() 的图象如图所示,有下列结论:
的图象如图所示,有下列结论:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.
其中,正确结论的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】
①首先根据抛物线开口向上,可得a>0;再根据对称轴在y轴的右边,判断出b<0;然后根据二次函数y=ax2+bx+c(a≠0)的图象与y轴的交点在y轴的负半轴,可得c<0,所以abc>0,据此判断即可.②根据抛物线的对称轴x=![]() =1,可得b+2a=0,据此判断即可.
=1,可得b+2a=0,据此判断即可.
③首先根据抛物线的对称轴是x=1,抛物线与x轴的一个交点2<x1<1,可得抛物线与x轴的另一个交点3<x2<4;然后根据x=4时,y>0,判断出8a+c>0即可.
④根据b+2a=0,可得b=2a,所以a+3b+c=a+3×(2a)+c=5a+c<0,据此判断即可.
∵抛物线开口向上,
∴a>0;
∵对称轴在y轴的右边,
∴b<0;
∵二次函数y=ax2+bx+c(a≠0)的图象与y轴的交点在y轴的负半轴,
∴c<0,
∴abc>0,
∴结论①正确;
∵抛物线的对称轴x=![]() =1,
=1,
∴b+2a=0,
∴结论②正确;
∵抛物线的对称轴是x=1,抛物线与x轴的一个交点2<x1<1,
∴抛物线与x轴的另一个交点3<x2<4;
∴x=4时,y>0,
∴16a+4b+c>0,
∵b+2a=0,
∴b=2a,
∴8a+c>0,
∴结论③正确;
∵b+2a=0,
∴b=2a,
∴a+3b+c=a+3×(2a)+c=5a+c<0,
∴结论④不正确.
综上,可得正确结论的个数是3个:①②③.
故选:C.


科目:初中数学 来源: 题型:
【题目】定义:如果两条线段将一个三角形分成3个等腰三角形,我们把这两条线段叫做这个三角形的三分线.
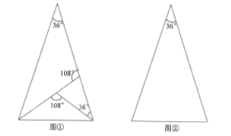
(1)图①是顶角为![]() 的等腰三角形,这个三角形的三分线已经画出,请你在图②中用不同于图①的方法画出顶角为
的等腰三角形,这个三角形的三分线已经画出,请你在图②中用不同于图①的方法画出顶角为![]() 的等腰三角形的三分线,并标注每个等腰三角形顶角的度数(若两种方法分得的三角形成3对全等三角形,则视为同一种);
的等腰三角形的三分线,并标注每个等腰三角形顶角的度数(若两种方法分得的三角形成3对全等三角形,则视为同一种);
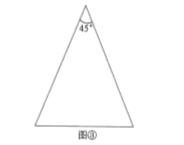
(2)图③是顶角为![]() 的等腰三角形,请你在图③中画出顶角为
的等腰三角形,请你在图③中画出顶角为![]() 的等腰三角形的三分线,并标注每个等腰三角形顶角的度数.
的等腰三角形的三分线,并标注每个等腰三角形顶角的度数.
(3)![]() 中,
中,![]() ,
,![]() 和
和![]() 是
是![]() 的三分线,点
的三分线,点![]() 在
在![]() 边上,点
边上,点![]() 在
在![]() 边上,且
边上,且![]() ,
,![]() ,设
,设![]() ,则
,则![]() 所有可能的值为_________.
所有可能的值为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了解市民对已闭幕的某一博览会的总体印象,利用最新引进的“计算机辅助电话访问系统”(简称CATI系统),采取电脑随机抽样的方式,对本市年龄在16~65岁之间的居民,进行了400个电话抽样调查.并根据每个年龄段的抽查人数和该年龄段对博览会总体印象感到满意的人数绘制了下面的图(1)和图(2)(部分)
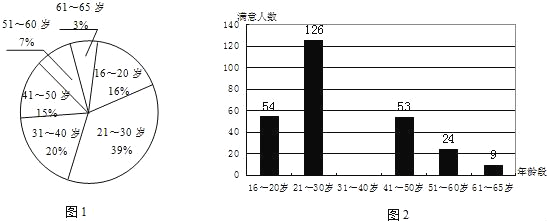
根据上图提供的信息回答下列问题:
(1)被抽查的居民中,人数最多的年龄段是 岁;
(2)已知被抽查的400人中有83%的人对博览会总体印象感到满意,请你求出31~40岁年龄段的满意人数,并补全图2.
注:某年龄段的满意率=该年龄段满意人数÷该年龄段被抽查人数×100%.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店购进A,B两种钢笔,若购进A种钢笔2支,B种钢笔3支,共需90元;购进A种钢笔3支,B种钢笔5支,共需145元.
(1)求A、B两种钢笔每支各多少元?
(2)若该文具店要购进A,B两种钢笔共90支,总费用不超过1588元,并且A种钢笔的数量少于B种钢笔的数量,那么该文具店有哪几种购买方案?
(3)文具店以每支30元的价格销售B种钢笔,很快销售一空,于是,文具店决定在进价不变的基础上再购进一批B种钢笔,涨价卖出,经统计,B种钢笔售价为30元时,每月可卖68支;每涨价1元,每月将少卖4支,设文具店将新购进的B种钢笔每支涨价a元(a为正整数),销售这批钢笔每月获利W元,试求W与a之间的函数关系式,并且求出B种铅笔销售单价定为多少元时,每月获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E为AB的中点,F为线段BE上任意一点,将线段EF绕点E逆时针旋转90°,得到线段EG.

(1)按请按要求补全图形:连接BG过点G作GH⊥BG,交对角线AC于点H,连接DH;
(2)判断DH与GH的数量关系并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各组条件中,能够判定△ABC≌△DEF 的是( )
A. ∠A=∠D,∠B=∠E,∠C=∠FB. AB=DE,BC=EF,∠A=∠D
C. ∠B=∠E=90°,BC=EF,AC=DFD. ∠A=∠D,AB=DF,∠B=∠E
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com