
【题目】定义:如果两条线段将一个三角形分成3个等腰三角形,我们把这两条线段叫做这个三角形的三分线.
(1)图①是顶角为![]() 的等腰三角形,这个三角形的三分线已经画出,请你在图②中用不同于图①的方法画出顶角为
的等腰三角形,这个三角形的三分线已经画出,请你在图②中用不同于图①的方法画出顶角为![]() 的等腰三角形的三分线,并标注每个等腰三角形顶角的度数(若两种方法分得的三角形成3对全等三角形,则视为同一种);
的等腰三角形的三分线,并标注每个等腰三角形顶角的度数(若两种方法分得的三角形成3对全等三角形,则视为同一种);
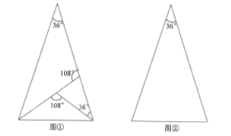
(2)图③是顶角为![]() 的等腰三角形,请你在图③中画出顶角为
的等腰三角形,请你在图③中画出顶角为![]() 的等腰三角形的三分线,并标注每个等腰三角形顶角的度数.
的等腰三角形的三分线,并标注每个等腰三角形顶角的度数.
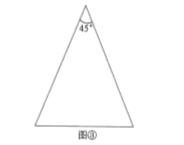
(3)![]() 中,
中,![]() ,
,![]() 和
和![]() 是
是![]() 的三分线,点
的三分线,点![]() 在
在![]() 边上,点
边上,点![]() 在
在![]() 边上,且
边上,且![]() ,
,![]() ,设
,设![]() ,则
,则![]() 所有可能的值为_________.
所有可能的值为_________.
【答案】(1)见详解;(2)见详解;(3)20或40.
【解析】
(1)作底角的平分线,再作底边的平行线,即可得到三分线;
(2)过底角定点作对边的高,形成一个等腰直角三角形和一个直角三角形,然后再构造一个等腰直角三角形,即可.
(3)根据题意,先确定30°角然后确定一边为BA,一边为BC,再固定BA的长,进而确定D点,分别考虑AD为等腰三角形的腰和底边,画出示意图,列出关于x的方程,即可得到答案.
(1)如图所示:
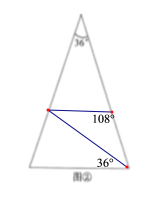
(2)如图所示:
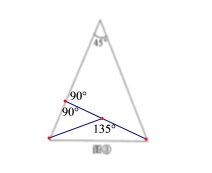
(3)①当AD=AE时,如图4,
∵![]() ,
,![]() ,
,
∴∠EDB=x°,
∴∠ADE=∠AED=2x°,
∵![]() ,
,
∴∠BAD=∠B=30°,
∴30+30=2x+x,
解得:x=20;
②当AD=DE时,如图5,
∵![]() ,
,![]() ,
,
∴∠EDB=x°,
∴∠DAE=∠AED=2x°,
∵![]() ,
,
∴∠BAD=∠B=30°,
∴30+30+2x+x=180,
解得:x=40.
③当AE=DE时,则∠EAD=∠EDA=![]() ,
,
∴∠ADC=∠EDA+∠EDC=(90-x)+x=90°
又∵∠ADC=30+30=60°,
∴这种情况不存在.
∴![]() 所有可能的值为20或40.
所有可能的值为20或40.
故答案是:20或40
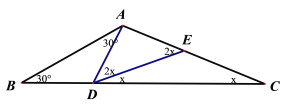
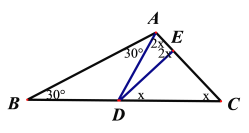
图4 图5


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:初中数学 来源: 题型:
【题目】如图,直角坐标系xOy中,一次函数y=﹣![]() x+5的图象l1分别与x,y轴交于A,B两点,正比例函数的图象l2与l1交于点C(m,4).
x+5的图象l1分别与x,y轴交于A,B两点,正比例函数的图象l2与l1交于点C(m,4).
(1)求m的值及l2的解析式;
(2)求S△AOC﹣S△BOC的值;
(3)一次函数y=kx+1的图象为l3,且11,l2,l3不能围成三角形,直接写出k的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
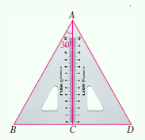
【题目】如图所示,将两个含30°角的三角尺摆放在一起,可以证得△ABD是等边三角形,于是我们得到:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.

交换命题的条件和结论,得到下面的命题:
在直角△ABC中,∠ACB=90°,如果![]() ,那么∠BAC=30°.
,那么∠BAC=30°.
请判断此命题的真假,若为真命题,请给出证明;若为假命题,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小华和小晶上山游玩,小华步行,小晶乘坐缆车,相约在山顶缆车的终点会合. 已知小华歩行的路程是缆车所经线路长的2倍,小晶在小华出发后50分钟才坐上缆车,缆车的平均速度为每分钟180米. 图中的折线反映了小华行走的路程![]() (米)与时间
(米)与时间![]() (分钟)之间的函数关系.
(分钟)之间的函数关系.
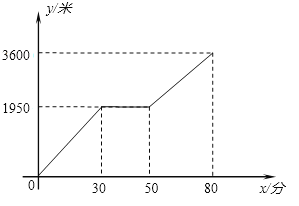
(1)小华行走的总路程是___________米,他途中休息了___________分钟;小华休息之后行走的速度是每分钟___________米;
(2)当![]() 时,
时,![]() 与
与![]() 的函数关系式是___________.
的函数关系式是___________.
(3)当小晶到达缆车终点时,小华离缆车终点的路程是___________米.
查看答案和解析>>
科目:初中数学 来源: 题型:
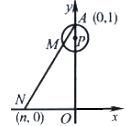
【题目】如图,在直角坐标系中,已知点A(0,1),点P在线段OA上,以AP为半径的⊙P周长为1.点M从A开始沿⊙P按逆时针方向转动,射线AM交x轴于点N(n,0),设点M转过的路程为m(0<m<1).随着点M的转动,当m从![]() 变化到
变化到![]() 时,点N相应移动的路径长为_______.
时,点N相应移动的路径长为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校在八年级新生中举行了全员参加的数学应用能力大赛,试卷题目共10题,每题10分.现分别从三个班中各随机取10名同学的成绩(单位:分),收集数据如下:
1班:90,70,80,80,80,80,80,90,80,100;
2班:70,80,80,80,60,90,90,90,100,90;
3班:90,60,70,80,80,80,80,90,100,100.
整理数据:
人数 班级 | 60分人数 | 70分人数 | 80分人数 | 90分人数 | 100分人数 |
1班 | 0 | 1 | 6 | 2 | 1 |
2班 | 1 | 1 | 3 |
| 1 |
3班 | 1 | 1 | 4 | 2 | 2 |
平均数 | 中位数 | 众数 | |
83 | 80 | 80 | |
2班 | 83 |
|
|
3班 |
| 80 | 80 |
分析数据:
根据以上信息回答下列问题:
(1)请直接写出表格中![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)比较这三组样本数据的平均数、中位数和众数,你认为哪个班的成绩比较好?请说明理由(写两条支持你结论的理由).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】科学考察队的一辆越野车需要穿越一片沙漠,但这辆车每次装满汽油最多只能行驶![]() ,队长想出一个方法,在沙漠中设若干个储油点(越野车穿越出沙漠,就可以另外加油).
,队长想出一个方法,在沙漠中设若干个储油点(越野车穿越出沙漠,就可以另外加油).
(1)如果穿越全程大于![]() 的沙漠,在沙漠中设一个储油点
的沙漠,在沙漠中设一个储油点![]() ,越野车装满油从起点
,越野车装满油从起点![]() 出发,到储油点
出发,到储油点![]() 时从车中取出部分油放进
时从车中取出部分油放进![]() 储油点,然后返回出发点,加满油后再开往
储油点,然后返回出发点,加满油后再开往![]() ,到
,到![]() 储油点时,取出储存的所有油放在车上,再从
储油点时,取出储存的所有油放在车上,再从![]() 出发到达终点,此时,这辆越野车穿越这片沙漠的最大行程是多少
出发到达终点,此时,这辆越野车穿越这片沙漠的最大行程是多少![]() ?
?
(2)如果穿越全程大于![]() 的沙漠,在沙漠中设2个储油点
的沙漠,在沙漠中设2个储油点![]() ,
,![]() ,越野车装满油从起点
,越野车装满油从起点![]() 出发,到储油点
出发,到储油点![]() 时从车中取出部分油放进
时从车中取出部分油放进![]() 储油点;然后返回出发点
储油点;然后返回出发点![]() 加满油,到储油点
加满油,到储油点![]() 时取出储油点
时取出储油点![]() 的全部油放到车上,再到达储油点
的全部油放到车上,再到达储油点![]() ,从车中取出部分油放进
,从车中取出部分油放进![]() 储油点;然后返回出发点
储油点;然后返回出发点![]() 加满油,到
加满油,到![]() 储油点取出储存的所有油放在车上,最后到达终点.此时,这辆越野车穿越这片沙漠的最大行程是多少
储油点取出储存的所有油放在车上,最后到达终点.此时,这辆越野车穿越这片沙漠的最大行程是多少![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数![]() 的图象与性质.
的图象与性质.
小东根据学习函数的经验,对函数![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小东的探究过程,请补充完成:
(1)化简函数解析式,当x≥-1时,y= ,当x<-1时y= ;
(2)根据(1)中的结果,请在所给坐标系中画出函数![]() 的图象;
的图象;
(3)结合函数图象,写出该函数的一条性质: .
(4)结合画出的函数图象,解决问题:若关于x的方程![]() 只有一个实数根,直接写出实数a的取值范围: .
只有一个实数根,直接写出实数a的取值范围: .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com