
����Ŀ��������һ�����⣺̽������![]() ��ͼ�������ʣ�
��ͼ�������ʣ�
С������ѧϰ�����ľ��飬�Ժ���![]() ��ͼ�������ʽ�����̽����
��ͼ�������ʽ�����̽����
������С����̽�����̣��벹����ɣ�
��1������������ʽ����x��-1ʱ��y���� ������x��-1ʱy���� ����
��2�����ݣ�1���еĽ����������������ϵ�л�������![]() ��ͼ��
��ͼ��
��3����Ϻ���ͼ��д���ú�����һ�����ʣ��� ����
��4����ϻ����ĺ���ͼ������⣺������x�ķ���![]() ֻ��һ��ʵ������ֱ��д��ʵ��a��ȡֵ��Χ���� ����
ֻ��һ��ʵ������ֱ��д��ʵ��a��ȡֵ��Χ���� ����
���𰸡���1��x��-1��2����������3����![]() ʱ��y��x�����������4��
ʱ��y��x�����������4��![]()
��������
��1�����ݾ���ֵ�����廯�ɣ�
��2�����ݣ�1���л���Ľ������ͼ�ɣ�
��3�����ͼ��شɣ�
��4������![]() �����ʣ����ͼ����.
�����ʣ����ͼ����.
��1�� ��x��-1ʱ��
![]() ��
��
��x��-1ʱ
![]() ��
��
(2)��ͼ��
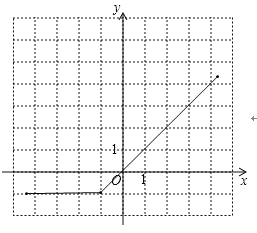
��3����������Сֵ-1�����������ֵ����![]() ʱ��y��x�������������𰸲�Ψһ��
ʱ��y��x�������������𰸲�Ψһ��
��3����![]() �����㣨0,1��
�����㣨0,1��
�൱![]() ʱ������
ʱ������![]() ֻ��һ��ʵ����.
ֻ��һ��ʵ����.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����ʵ����Ժ���������ǿͬ־����ʩ����ʱ��ָʾ����,�������ί�������ֳ�̨��һϵ�С���ũ���Ż�����,ʹũ��������������.ijũ����������һ��ũ����Ʒ,��֪���ֲ�Ʒ�ijɱ���Ϊ20Ԫ/ǧ��.�г����鷢��,�ò�Ʒÿ�����������(ǧ��)�����ۼ�x(Ԫ/ǧ��)�����¹�ϵ:��=��2x��80.�����ֲ�Ʒÿ�����������Ϊ��(Ԫ).
(1)�����x֮��ĺ�����ϵʽ.
(2)�����ۼ۶�Ϊ����Ԫʱ,ÿ��������������?��������Ƕ���?
(3)�����۲��Ź涨���ֲ�Ʒ�����ۼ۲��ø���28Ԫ/ǧ��,��ũ����Ҫÿ����150Ԫ����������,���ۼ�Ӧ��Ϊ����Ԫ?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺��������߶ν�һ�������ηֳ�3�����������Σ����ǰ��������߶�������������ε�������.
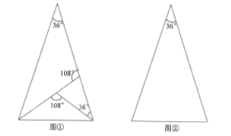
��1��ͼ���Ƕ���Ϊ![]() �ĵ��������Σ���������ε��������Ѿ�������������ͼ�����ò�ͬ��ͼ�ٵķ�����������Ϊ
�ĵ��������Σ���������ε��������Ѿ�������������ͼ�����ò�ͬ��ͼ�ٵķ�����������Ϊ![]() �ĵ��������ε������ߣ�����עÿ�����������ζ��ǵĶ����������ַ����ֵõ������γ�3��ȫ�������Σ�����Ϊͬһ�֣���
�ĵ��������ε������ߣ�����עÿ�����������ζ��ǵĶ����������ַ����ֵõ������γ�3��ȫ�������Σ�����Ϊͬһ�֣���
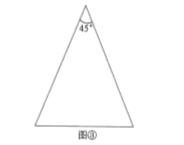
��2��ͼ���Ƕ���Ϊ![]() �ĵ��������Σ�������ͼ���л�������Ϊ
�ĵ��������Σ�������ͼ���л�������Ϊ![]() �ĵ��������ε������ߣ�����עÿ�����������ζ��ǵĶ���.
�ĵ��������ε������ߣ�����עÿ�����������ζ��ǵĶ���.
��3��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �������ߣ���
�������ߣ���![]() ��
��![]() ���ϣ���
���ϣ���![]() ��
��![]() ���ϣ���
���ϣ���![]() ��
��![]() ����
����![]() ����
����![]() ���п��ܵ�ֵΪ_________.
���п��ܵ�ֵΪ_________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijС��ҵΪ�ӿ��ҵת����������������һ��A��B�����ͺŵĻ�������֪һ̨A�ͻ�����һ̨B�ͻ���ÿСʱ��ӹ�2���������һ̨A�ͻ����ӹ�80�������һ̨B�ͻ����ӹ�60���������ʱ����ȣ�
��1��ÿ̨A��B�����ͺŵĻ���ÿСʱ�ֱ�ӹ����ٸ������
��2���������ҵ�ƻ�����A��B�����ͺŵĻ�����10̨һ��ӹ�һ���������Ϊ�������������Ҫ�����ֻ���ÿСʱ�ӹ������������72����ͬʱΪ�˱��ϻ�����������ת�����ֻ���ÿСʱ�ӹ���������ܳ���76������ôA��B�����ͺŵĻ������Ը����Ŷ���̨��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס���������ֱ���ܵ��ϴ�![]() ��
��![]() ͬ�������ܲ���
ͬ�������ܲ���![]() �����800�ף���֪���ȳ���
�����800�ף���֪���ȳ���![]() �����ȵ��յ��ԭ����Ϣ��3�룬�������������Ľϴ�������ԭ���ٶȵ�
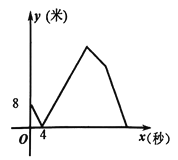
�����ȵ��յ��ԭ����Ϣ��3�룬�������������Ľϴ�������ԭ���ٶȵ�![]() �����ٷ��أ�ֱ���������˵ڶ�������ʱ����ͬʱֹͣ�˶������ܲ������У��ס�������֮��ľ���
�����ٷ��أ�ֱ���������˵ڶ�������ʱ����ͬʱֹͣ�˶������ܲ������У��ס�������֮��ľ���![]() ���ף����ҳ�����ʱ��
���ף����ҳ�����ʱ��![]() ���룩֮��Ĺ�ϵ��ͼ��ʾ����ס�������������֮��ľ���Ϊ____________��.
���룩֮��Ĺ�ϵ��ͼ��ʾ����ס�������������֮��ľ���Ϊ____________��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
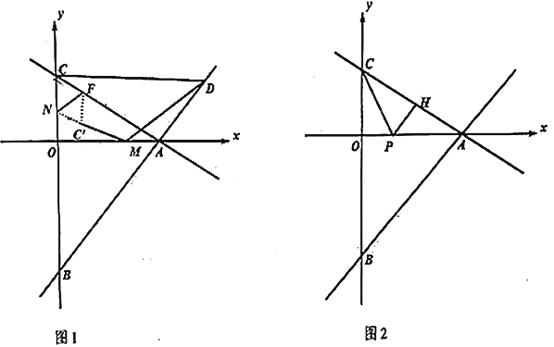
����Ŀ����ͼ1����ֱ֪��![]() ��ֱ��
��ֱ��![]() ����
����![]() ����һ��
����һ��![]() ���ҷֱ�
���ҷֱ�![]() ���ڵ�
���ڵ�![]() ����
����![]() ����
����![]() .
.
��1����![]() ��ֵ��
��ֵ��
��2����ͼ1����![]() ��ֱ��
��ֱ��![]() ��һ�㣬����
��һ�㣬����![]() ���Ϸ�����
���Ϸ�����![]() ʱ�����߶�
ʱ�����߶�![]() ��ȡһ��
��ȡһ��![]() ��ʹ��
��ʹ��![]() ����
����![]() �ֱ�Ϊ
�ֱ�Ϊ![]() �ᡢ
�ᡢ![]() ���ϵĶ��㣬����
���ϵĶ��㣬����![]() ����
����![]() ��
��![]() ������
������![]() ����
����![]() ����Сֵ��
����Сֵ��
��3����ͼ2��![]() �ֱ�Ϊ����
�ֱ�Ϊ����![]() �ϵĶ��㣬����
�ϵĶ��㣬����![]() �Ƿ���������ĵ�
�Ƿ���������ĵ�![]() ��ʹ��
��ʹ��![]() Ϊ���������Σ�
Ϊ���������Σ�![]() Ϊֱ��������ͬʱ����.��ֱ��д�����������ĵ�
Ϊֱ��������ͬʱ����.��ֱ��д�����������ĵ�![]() ����.
����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ϊ�˽�������ѱ�Ļ��ijһ�����������ӡ����������������������������绰����ϵͳ�������CATIϵͳ������ȡ������������ķ�ʽ���Ա���������16��65��֮��ľ�������400���绰�������飮������ÿ������εij������������ζԲ���������ӡ��е���������������������ͼ��1����ͼ��2�������֣�
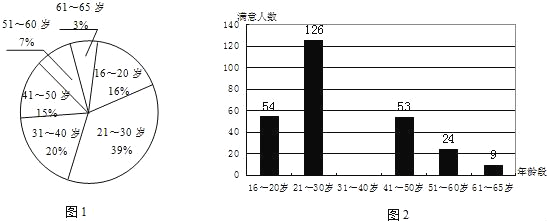
������ͼ�ṩ����Ϣ�ش��������⣺
��1�������ľ����У������������������ ���ꣻ
��2����֪������400������83%���˶Բ���������ӡ��е����⣬�������31��40������ε���������������ȫͼ2��
ע��ij����ε�������=�����������������������α����������100%��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1��|��2|+![]() tan30��+��2018���У�0-��
tan30��+��2018����0-��![]() ��-1
��-1
��2���Ȼ�������ֵ����![]() ��1����
��1����![]() ������x��ֵ�Ӳ���ʽ��
������x��ֵ�Ӳ���ʽ��![]() ����������ѡȡ��
����������ѡȡ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и��������У��ܹ��ж���ABC�ա�DEF ���ǣ� ��
A. ��A����D����B����E����C����FB. AB��DE��BC��EF����A����D
C. ��B����E��90�㣬BC��EF��AC��DFD. ��A����D��AB��DF����B����E
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com