练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

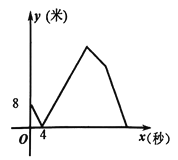
    【题目】甲、乙两人在直线跑道上从向同向匀速跑步，间相距800米，已知甲先出发，乙先到终点后原地休息了3秒，由于乙体力消耗较大，于是以原来速度的倍匀速返回，直到甲乙两人第二次相遇时两人同时停止运动。在跑步过程中，甲、乙两人之间的距离（米）与乙出发的时间（秒）之间的关系如图所示，则甲、乙两次相遇点之间的距离为____________米.

    【答案】696

    【解析】

    首先根据图象分别求出甲乙的速度，然后求出第二次相遇时甲乙所行驶的距离，即可得解.

    由图象得甲的速度为米/秒

    乙的速度为米/秒

    乙从第一次相遇后到终点所用时间为秒

    乙先到终点后原地休息了3秒，此时甲行驶的距离为米

    此时甲乙相距800-672=128米

    乙反向行驶的速度为米/秒

    甲乙第二次相遇所经过时间为秒

    此时乙反向行驶的距离为8×8=64米

    甲乙两次相遇点之间的距离为800-64-40=696米

    故答案为696米.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某市2018年平均每天的垃圾处理量为40万吨/天，2019年平均每天的垃圾排放量比2018年平均每天的垃圾排放量多100万吨；2019年平均每天的垃圾处理量是2018年平均每天的垃圾处理量的2. 5倍. 若2019年平均每天的垃圾处理率是2018年平均每天的垃圾处理率的1. 25倍.

    （注：）

    （1）求该市2018年平均每天的垃圾排放量；

    （2）预计该市2020年平均每天的垃圾排放量比2019年平均每天的垃圾排放量增加. 如果按照创卫要求“城市平均每天的垃圾处理率不低于”，那么该市2020年平均每天的垃圾处理量在2019年平均每天的垃圾处理量的基础上，至少还需要増加多少万吨才能使该市2020年平均每天的垃圾处理率符合创卫的要求？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

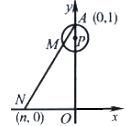
    【题目】如图，在直角坐标系中，已知点A（0，1），点P在线段OA上，以AP为半径的⊙P周长为1．点M从A开始沿⊙P按逆时针方向转动，射线AM交x轴于点N（n，0），设点M转过的路程为m（0＜m＜1）．随着点M的转动，当m从变化到时，点N相应移动的路径长为_______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】科学考察队的一辆越野车需要穿越一片沙漠，但这辆车每次装满汽油最多只能行驶，队长想出一个方法，在沙漠中设若干个储油点（越野车穿越出沙漠，就可以另外加油）.

    （1）如果穿越全程大于的沙漠，在沙漠中设一个储油点，越野车装满油从起点出发，到储油点时从车中取出部分油放进储油点，然后返回出发点，加满油后再开往，到储油点时，取出储存的所有油放在车上，再从出发到达终点，此时，这辆越野车穿越这片沙漠的最大行程是多少？

    （2）如果穿越全程大于的沙漠，在沙漠中设2个储油点，，越野车装满油从起点出发，到储油点时从车中取出部分油放进储油点；然后返回出发点加满油，到储油点时取出储油点的全部油放到车上，再到达储油点，从车中取出部分油放进储油点；然后返回出发点加满油，到储油点取出储存的所有油放在车上，最后到达终点.此时，这辆越野车穿越这片沙漠的最大行程是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，A（-5，0），B（-3，0），点C在y轴的正半轴上，∠CBO=45°，CD∥AB．∠CDA=90°．点P从点Q（4，0）出发，沿x轴向左以每秒1个单位长度的速度运动，运动时时间t秒．

    （1）求点C的坐标；

    （2）当∠BCP=15°时，求t的值；

    （3）以点P为圆心，PC为半径的⊙P随点P的运动而变化，当⊙P与四边形ABCD的边（或边所在的直线）相切时，求t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】有这样一个问题：探究函数的图象与性质．

    小东根据学习函数的经验，对函数的图象与性质进行了探究．

    下面是小东的探究过程，请补充完成：

    （1）化简函数解析式，当x≥-1时，y＝　 　，当x＜-1时y＝　 　；

    （2）根据（1）中的结果，请在所给坐标系中画出函数的图象；

    （3）结合函数图象，写出该函数的一条性质：　 　．

    （4）结合画出的函数图象，解决问题：若关于x的方程只有一个实数根，直接写出实数a的取值范围：　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，，是分别沿着边翻折形成的.若，与交于点，则的度数为（ ）

    A.15°B.20°C.30°D.36°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点O是等边△ABC内一点，D是△ABC外的一点，∠AOB＝110°，∠BOC＝α，△BOC≌△ADC，∠OCD＝60°，连接OD．

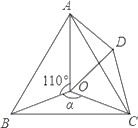
    （1）求证：△OCD是等边三角形；

    （2）当α＝150°时，试判断△AOD的形状，并说明理由；

    （3）探究：当α为多少度时，△AOD是等腰三角形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，圆柱形杯子高9cm，底面周长18cm，在杯口点B处有一滴蜂蜜，此时蚂蚁在杯外底部与蜂蜜相对的点A处．

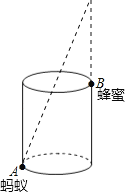
    （1）求蚂蚁从A到B处杯壁爬行吃到蜂蜜的最短距离；

    （2）若蚂蚁出发时发现有蜂蜜正以每秒钟1cm沿杯内壁下滑，蚂蚁出发后3秒钟吃到了蜂蜜，求蚂蚁的平均速度至少是多少？

    查看答案和解析>>

    同步练习册答案