
ЁОЬтФПЁПаЁЛЊКЭаЁОЇЩЯЩНгЮЭцЃЌаЁЛЊВНааЃЌаЁОЇГЫзјРТГЕЃЌЯрдМдкЩНЖЅРТГЕЕФжеЕуЛсКЯ. вбжЊаЁЛЊiааЕФТЗГЬЪЧРТГЕЫљОЯпТЗГЄЕФ2БЖЃЌаЁОЇдкаЁЛЊГіЗЂКѓ50ЗжжгВХзјЩЯРТГЕЃЌРТГЕЕФЦНОљЫйЖШЮЊУПЗжжг180Уз. ЭМжаЕФелЯпЗДгГСЫаЁЛЊаазпЕФТЗГЬ![]() ЃЈУзЃЉгыЪБМф
ЃЈУзЃЉгыЪБМф![]() ЃЈЗжжгЃЉжЎМфЕФКЏЪ§ЙиЯЕ.
ЃЈЗжжгЃЉжЎМфЕФКЏЪ§ЙиЯЕ.
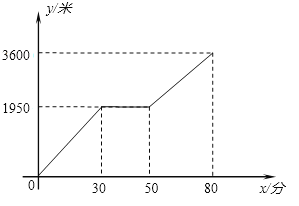
ЃЈ1ЃЉаЁЛЊаазпЕФзмТЗГЬЪЧ___________УзЃЌЫћЭОжаанЯЂСЫ___________ЗжжгЃЛаЁЛЊанЯЂжЎКѓаазпЕФЫйЖШЪЧУПЗжжг___________УзЃЛ
ЃЈ2ЃЉЕБ![]() ЪБЃЌ
ЪБЃЌ![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕЪНЪЧ___________.
ЕФКЏЪ§ЙиЯЕЪНЪЧ___________.
ЃЈ3ЃЉЕБаЁОЇЕНДяРТГЕжеЕуЪБЃЌаЁЛЊРыРТГЕжеЕуЕФТЗГЬЪЧ___________Уз.
ЁОД№АИЁПЃЈ1ЃЉ3600ЃЌ20ЃЌ55ЃЛЃЈ2ЃЉy=65xЃЛЃЈ3ЃЉ1100
ЁОНтЮіЁП
ИљОнЭМЯѓЛёШЁаХЯЂЃК
ЃЈ1ЃЉаЁЛЊЕНДяЩНЖЅгУЪБ80ЗжжгЃЌжаЭОанЯЂСЫ20ЗжжгЃЌааГЬЮЊ3600УзЃЛанЯЂЧА30Зжжгаазп1950УзЃЌанЯЂКѓ30ЗжжгаазпЃЈ3600-1950ЃЉУзЃЌРћгУТЗГЬЁЂЪБМфЕУГіЫйЖШМДПЩЃЎ
ЃЈ2ЃЉРћгУД§ЖЈЯЕЪ§ЗЈНтД№е§БШР§КЏЪ§НтЮіЪНМДПЩЃЛ
ЃЈ3ЃЉЧѓаЁОЇЕНДяРТГЕжеЕуЕФЪБМфЃЌМЦЫуаЁЛЊаазпТЗГЬЃЌЧѓРыРТГЕжеЕуЕФТЗГЬЃЎ
НтЃКЃЈ1ЃЉИљОнЭМЯѓжЊЃКаЁЛЊаазпЕФзмТЗГЬЪЧ 3600УзЃЌЫћЭОжаанЯЂСЫ 20ЗжжгЃЛаЁЛЊанЯЂжЎКѓаазпЕФЫйЖШЪЧЃЈ3600-1950ЃЉЁТЃЈ80-50ЃЉ=55Уз/ЗжжгЃЌ
ЙЪД№АИЮЊ 3600ЃЌ20ЃЌ55ЃЛ
ЃЈ2ЃЉЩшКЏЪ§ЙиЯЕЪНЮЊy=kxЃЌ
ПЩЕУЃК1950=30kЃЌ
НтЕУЃКk=65ЃЌ
ЫљвдНтЮіЪНЮЊЃКy=65xЃЌ
ЙЪД№АИЮЊЃКy=65xЃЛ
ЃЈ3ЃЉаЁОЇЫљгУЪБМфЃК![]() ЃЌ
ЃЌ
аЁЛЊЕНДяЩНЖЅгУЪБ80ЗжжгЃЌ
аЁЛЊБШаЁОЇГйЕН80-50-10=20ЃЈЗжЃЉЃЌ
ЁраЁОЇЕНДяжеЕуЪБЃЌаЁЛЊРыРТГЕжеЕуЕФТЗГЬЮЊЃК20ЁС55=1100ЃЈУзЃЉЃЌ
ЙЪД№АИЮЊЃК1100ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
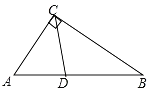
ЁОЬтФПЁПШчЭМЃЌОиаЮABCDжаЃЌEЃЌFЗжБ№ЪЧЯпЖЮBCЃЌADЕФжаЕуЃЌAB=2ЃЌAD=4ЃЌЖЏЕуPбиECЃЌCDЃЌDFЕФТЗЯпгЩЕуEдЫЖЏЕНЕуFЃЌдђЁїPABЕФУцЛ§sЪЧЖЏЕуPдЫЖЏЕФТЗОЖзмГЄxЕФКЏЪ§ЃЌетИіКЏЪ§ЕФДѓжТЭМЯѓПЩФмЪЧ
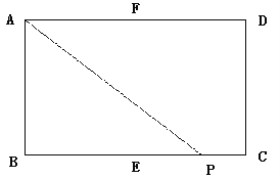
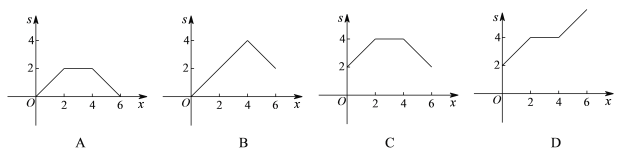
A. A B. B C. C D. D
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫТфЪЕЙњЮёдКИБзмРэРюПЫЧПЭЌжОЕНЖїЪЉПМВьЪБЕФжИЪООЋЩё,зюНќЃЌжнЮЏжнеўИЎгжГіЬЈСЫвЛЯЕСаЁАШ§ХЉЁБгХЛнеўВп,ЪЙХЉУёЪеШыДѓЗљЖШдіМг.ФГХЉЛЇЩњВњОЯњвЛжжХЉИБВњЦЗ,вбжЊетжжВњЦЗЕФГЩБОМлЮЊ20дЊ/ЧЇПЫ.ЪаГЁЕїВщЗЂЯж,ИУВњЦЗУПЬьЕФЯњЪлСПЃї(ЧЇПЫ)гыЯњЪлМлx(дЊ/ЧЇПЫ)гаШчЯТЙиЯЕ:Ѓї=Ѓ2xЃЋ80.ЩшетжжВњЦЗУПЬьЕФЯњЪлРћШѓЮЊЃљ(дЊ).
(1)ЧѓЃљгыxжЎМфЕФКЏЪ§ЙиЯЕЪН.
(2)ЕБЯњЪлМлЖЈЮЊЖрЩйдЊЪБ,УПЬьЕФЯњЪлРћШѓзюДѓ?зюДѓРћШѓЪЧЖрЩй?
(3)ШчЙћЮяМлВПУХЙцЖЈетжжВњЦЗЕФЯњЪлМлВЛЕУИпгк28дЊ/ЧЇПЫ,ИУХЉЛЇЯывЊУПЬьЛёЕУ150дЊЕФЯњЪлРћШѓ,ЯњЪлМлгІЖЈЮЊЖрЩйдЊ?
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
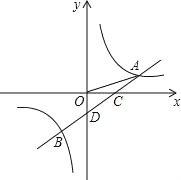
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§y=ax+bЕФЭМЯѓгыЗДБШР§КЏЪ§![]() ЕФЭМЯѓНЛгкAЃЌBСНЕуЃЌгыXжсНЛгкЕуCЃЌгыYжсНЛгкЕуDЃЌвбжЊ
ЕФЭМЯѓНЛгкAЃЌBСНЕуЃЌгыXжсНЛгкЕуCЃЌгыYжсНЛгкЕуDЃЌвбжЊ![]() ЃЌAЃЈnЃЌ1ЃЉЃЌЕуBЕФзјБъЮЊЃЈЉ2ЃЌmЃЉ
ЃЌAЃЈnЃЌ1ЃЉЃЌЕуBЕФзјБъЮЊЃЈЉ2ЃЌmЃЉ
ЃЈ1ЃЉЧѓЗДБШР§КЏЪ§ЕФНтЮіЪНКЭвЛДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉСЌНсBOЃЌЧѓЁїAOBЕФУцЛ§ЃЛ
ЃЈ3ЃЉЙлВьЭМЯѓжБНгаДГівЛДЮКЏЪ§ЕФжЕДѓгкЗДБШР§КЏЪ§ЕФжЕЪБxЕФШЁжЕЗЖЮЇЪЧЁЁ ЁЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊдк![]() жаЃЌ
жаЃЌ![]() ЦНЗж
ЦНЗж![]() ЃЌ
ЃЌ![]() ЃЌдђ
ЃЌдђ![]() ___________. ЃЈгУКЌ
___________. ЃЈгУКЌ![]() ЕФДњЪ§ЪНБэЪОЃЉ.
ЕФДњЪ§ЪНБэЪОЃЉ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
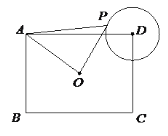
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCDжаЃЌAB=3ЃЌBC=4ЃЌOЮЊОиаЮABCDЕФжааФЃЌвдDЮЊдВаФ1ЮЊАыОЖзїЁбDЃЌPЮЊЁбDЩЯЕФвЛИіЖЏЕуЃЌСЌНгAPЁЂOPЃЌдђЁїAOPУцЛ§ЕФзюДѓжЕЮЊЃЈЁЁЁЁЃЉ
A. 4 B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖЈвхЃКШчЙћСНЬѕЯпЖЮНЋвЛИіШ§НЧаЮЗжГЩ3ИіЕШбќШ§НЧаЮЃЌЮвУЧАбетСНЬѕЯпЖЮНазіетИіШ§НЧаЮЕФШ§ЗжЯп.
ЃЈ1ЃЉЭМЂйЪЧЖЅНЧЮЊ![]() ЕФЕШбќШ§НЧаЮЃЌетИіШ§НЧаЮЕФШ§ЗжЯпвбОЛГіЃЌЧыФудкЭМЂкжагУВЛЭЌгкЭМЂйЕФЗНЗЈЛГіЖЅНЧЮЊ
ЕФЕШбќШ§НЧаЮЃЌетИіШ§НЧаЮЕФШ§ЗжЯпвбОЛГіЃЌЧыФудкЭМЂкжагУВЛЭЌгкЭМЂйЕФЗНЗЈЛГіЖЅНЧЮЊ![]() ЕФЕШбќШ§НЧаЮЕФШ§ЗжЯпЃЌВЂБъзЂУПИіЕШбќШ§НЧаЮЖЅНЧЕФЖШЪ§ЃЈШєСНжжЗНЗЈЗжЕУЕФШ§НЧаЮГЩ3ЖдШЋЕШШ§НЧаЮЃЌдђЪгЮЊЭЌвЛжжЃЉЃЛ
ЕФЕШбќШ§НЧаЮЕФШ§ЗжЯпЃЌВЂБъзЂУПИіЕШбќШ§НЧаЮЖЅНЧЕФЖШЪ§ЃЈШєСНжжЗНЗЈЗжЕУЕФШ§НЧаЮГЩ3ЖдШЋЕШШ§НЧаЮЃЌдђЪгЮЊЭЌвЛжжЃЉЃЛ
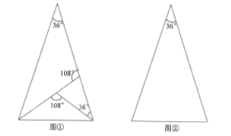
ЃЈ2ЃЉЭМЂлЪЧЖЅНЧЮЊ![]() ЕФЕШбќШ§НЧаЮЃЌЧыФудкЭМЂлжаЛГіЖЅНЧЮЊ
ЕФЕШбќШ§НЧаЮЃЌЧыФудкЭМЂлжаЛГіЖЅНЧЮЊ![]() ЕФЕШбќШ§НЧаЮЕФШ§ЗжЯпЃЌВЂБъзЂУПИіЕШбќШ§НЧаЮЖЅНЧЕФЖШЪ§.
ЕФЕШбќШ§НЧаЮЕФШ§ЗжЯпЃЌВЂБъзЂУПИіЕШбќШ§НЧаЮЖЅНЧЕФЖШЪ§.
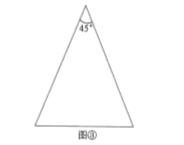
ЃЈ3ЃЉ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() КЭ
КЭ![]() ЪЧ
ЪЧ![]() ЕФШ§ЗжЯпЃЌЕу
ЕФШ§ЗжЯпЃЌЕу![]() дк
дк![]() БпЩЯЃЌЕу
БпЩЯЃЌЕу![]() дк
дк![]() БпЩЯЃЌЧв
БпЩЯЃЌЧв![]() ЃЌ
ЃЌ![]() ЃЌЩш
ЃЌЩш![]() ЃЌдђ
ЃЌдђ![]() ЫљгаПЩФмЕФжЕЮЊ_________.
ЫљгаПЩФмЕФжЕЮЊ_________.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЁЮЂЦѓвЕЮЊМгПьВњвЕзЊаЭЩ§МЖВНЗЅЃЌв§НјвЛХњAЃЌBСНжжаЭКХЕФЛњЦїЃЎвбжЊвЛЬЈAаЭЛњЦїБШвЛЬЈBаЭЛњЦїУПаЁЪБЖрМгЙЄ2ИіСуМўЃЌЧввЛЬЈAаЭЛњЦїМгЙЄ80ИіСуМўгывЛЬЈBаЭЛњЦїМгЙЄ60ИіСуМўЫљгУЪБМфЯрЕШЃЎ
ЃЈ1ЃЉУПЬЈAЃЌBСНжжаЭКХЕФЛњЦїУПаЁЪБЗжБ№МгЙЄЖрЩйИіСуМўЃП
ЃЈ2ЃЉШчЙћИУЦѓвЕМЦЛЎАВХХAЃЌBСНжжаЭКХЕФЛњЦїЙВ10ЬЈвЛЦ№МгЙЄвЛХњИУСуМўЃЌЮЊСЫШчЦкЭъГЩШЮЮёЃЌвЊЧѓСНжжЛњЦїУПаЁЪБМгЙЄЕФСуМўВЛЩйгк72МўЃЌЭЌЪБЮЊСЫБЃеЯЛњЦїЕФе§ГЃдЫзЊЃЌСНжжЛњЦїУПаЁЪБМгЙЄЕФСуМўВЛФмГЌЙ§76МўЃЌФЧУДAЃЌBСНжжаЭКХЕФЛњЦїПЩвдИїАВХХЖрЩйЬЈЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ1ЃЉ|Љ2|+![]() tan30Ёу+ЃЈ2018ЉІаЃЉ0-ЃЈ
tan30Ёу+ЃЈ2018ЉІаЃЉ0-ЃЈ![]() ЃЉ-1
ЃЉ-1
ЃЈ2ЃЉЯШЛЏМђЃЌдйЧѓжЕЃКЃЈ![]() Љ1ЃЉЁТ
Љ1ЃЉЁТ![]() ЃЌЦфжаxЕФжЕДгВЛЕШЪНзщ
ЃЌЦфжаxЕФжЕДгВЛЕШЪНзщ![]() ЕФећЪ§НтжабЁШЁЃЎ
ЕФећЪ§НтжабЁШЁЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com