
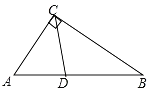
【题目】如图,已知在![]() 中,
中,![]() 平分
平分![]() ,
,![]() ,则
,则![]() ___________. (用含
___________. (用含![]() 的代数式表示).
的代数式表示).
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:
【题目】阅读下面材料,完成后面题目.
0°-360°间的角的三角函数
在初中,我们学习过锐角的正弦、余弦、正切和余切四种三角函数,即在图1所示的直角三角形ABC,∠A是锐角,那么sinA=![]() ,cosA=
,cosA=![]() ,tanA=
,tanA=![]() ,cotA=
,cotA=![]()
为了研究需要,我们再从另一个角度来规定一个角的三角函数的意义:
设有一个角α,我们以它的顶点作为原点,以它的始边作为x轴的正半轴ox,建立直角坐标系(图2),在角α的终边上任取一点P,它的横坐标是x,纵坐标是y,点P和原点(0,0)的距离为r=![]() (r总是正的),然后把角α的三角函数规定为:sinα=
(r总是正的),然后把角α的三角函数规定为:sinα=![]() ,cosα=
,cosα=![]() ,tanα=
,tanα=![]() ,cotα=
,cotα=![]()
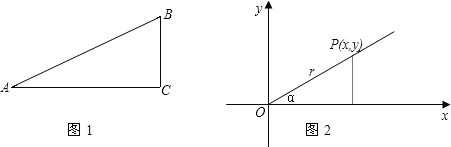
我们知道,图1的四个比值的大小与角A的大小有关,而与直角三角形的大小无关,同样图2中四个比值的大小也仅与角α的大小有关,而与点P在角α的终边位置无关.
比较图1与图2,可以看出一个角的三角函数的意义的两种规定实际上是一样的,根据第二种定义回答下列问题.
(1)若90°<α<180°,则角α的三角函数值sinα、cosα、tanα、cotα,其中取正值的是哪几个?
(2)若角α的终边与直线y=2x重合,求sinα+cosα的值.
(3)若角α是钝角,其终边上一点P(x,![]() ),且cosα=
),且cosα=![]() x,求tanα的值.
x,求tanα的值.
(4)若0°≤α≤90°,求sinα+cosα的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市2018年平均每天的垃圾处理量为40万吨/天,2019年平均每天的垃圾排放量比2018年平均每天的垃圾排放量多100万吨;2019年平均每天的垃圾处理量是2018年平均每天的垃圾处理量的2. 5倍. 若2019年平均每天的垃圾处理率是2018年平均每天的垃圾处理率的1. 25倍.
(注:![]() )
)
(1)求该市2018年平均每天的垃圾排放量;
(2)预计该市2020年平均每天的垃圾排放量比2019年平均每天的垃圾排放量增加![]() . 如果按照创卫要求“城市平均每天的垃圾处理率不低于
. 如果按照创卫要求“城市平均每天的垃圾处理率不低于![]() ”,那么该市2020年平均每天的垃圾处理量在2019年平均每天的垃圾处理量的基础上,至少还需要増加多少万吨才能使该市2020年平均每天的垃圾处理率符合创卫的要求?
”,那么该市2020年平均每天的垃圾处理量在2019年平均每天的垃圾处理量的基础上,至少还需要増加多少万吨才能使该市2020年平均每天的垃圾处理率符合创卫的要求?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,将两个含30°角的三角尺摆放在一起,可以证得△ABD是等边三角形,于是我们得到:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
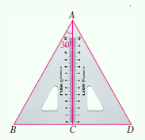

交换命题的条件和结论,得到下面的命题:
在直角△ABC中,∠ACB=90°,如果![]() ,那么∠BAC=30°.
,那么∠BAC=30°.
请判断此命题的真假,若为真命题,请给出证明;若为假命题,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法错误的是( )
A.到点![]() 距离等于
距离等于![]() 的点的轨迹是以点
的点的轨迹是以点![]() 为圆心,半径长为
为圆心,半径长为![]() 的圆
的圆
B.等腰![]() 的底边
的底边![]() 固定,顶点
固定,顶点![]() 的轨迹是线段
的轨迹是线段![]() 的垂直平分线
的垂直平分线
C.在一个角的内部(包括顶点)到角的两边距离相等的点的轨边是这个角的平分线
D.到直线![]() 距离等于
距离等于![]() 的点的轨迹是两条平行于
的点的轨迹是两条平行于![]() 且与
且与![]() 的距离等于
的距离等于![]() 的直线
的直线
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小华和小晶上山游玩,小华步行,小晶乘坐缆车,相约在山顶缆车的终点会合. 已知小华歩行的路程是缆车所经线路长的2倍,小晶在小华出发后50分钟才坐上缆车,缆车的平均速度为每分钟180米. 图中的折线反映了小华行走的路程![]() (米)与时间
(米)与时间![]() (分钟)之间的函数关系.
(分钟)之间的函数关系.
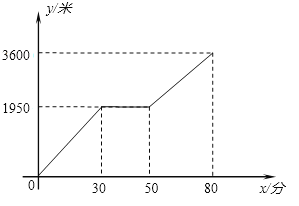
(1)小华行走的总路程是___________米,他途中休息了___________分钟;小华休息之后行走的速度是每分钟___________米;
(2)当![]() 时,
时,![]() 与
与![]() 的函数关系式是___________.
的函数关系式是___________.
(3)当小晶到达缆车终点时,小华离缆车终点的路程是___________米.
查看答案和解析>>
科目:初中数学 来源: 题型:
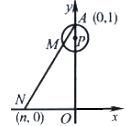
【题目】如图,在直角坐标系中,已知点A(0,1),点P在线段OA上,以AP为半径的⊙P周长为1.点M从A开始沿⊙P按逆时针方向转动,射线AM交x轴于点N(n,0),设点M转过的路程为m(0<m<1).随着点M的转动,当m从![]() 变化到
变化到![]() 时,点N相应移动的路径长为_______.
时,点N相应移动的路径长为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】科学考察队的一辆越野车需要穿越一片沙漠,但这辆车每次装满汽油最多只能行驶![]() ,队长想出一个方法,在沙漠中设若干个储油点(越野车穿越出沙漠,就可以另外加油).
,队长想出一个方法,在沙漠中设若干个储油点(越野车穿越出沙漠,就可以另外加油).
(1)如果穿越全程大于![]() 的沙漠,在沙漠中设一个储油点
的沙漠,在沙漠中设一个储油点![]() ,越野车装满油从起点
,越野车装满油从起点![]() 出发,到储油点
出发,到储油点![]() 时从车中取出部分油放进
时从车中取出部分油放进![]() 储油点,然后返回出发点,加满油后再开往
储油点,然后返回出发点,加满油后再开往![]() ,到
,到![]() 储油点时,取出储存的所有油放在车上,再从
储油点时,取出储存的所有油放在车上,再从![]() 出发到达终点,此时,这辆越野车穿越这片沙漠的最大行程是多少
出发到达终点,此时,这辆越野车穿越这片沙漠的最大行程是多少![]() ?
?
(2)如果穿越全程大于![]() 的沙漠,在沙漠中设2个储油点
的沙漠,在沙漠中设2个储油点![]() ,
,![]() ,越野车装满油从起点
,越野车装满油从起点![]() 出发,到储油点
出发,到储油点![]() 时从车中取出部分油放进
时从车中取出部分油放进![]() 储油点;然后返回出发点
储油点;然后返回出发点![]() 加满油,到储油点
加满油,到储油点![]() 时取出储油点
时取出储油点![]() 的全部油放到车上,再到达储油点
的全部油放到车上,再到达储油点![]() ,从车中取出部分油放进
,从车中取出部分油放进![]() 储油点;然后返回出发点
储油点;然后返回出发点![]() 加满油,到
加满油,到![]() 储油点取出储存的所有油放在车上,最后到达终点.此时,这辆越野车穿越这片沙漠的最大行程是多少
储油点取出储存的所有油放在车上,最后到达终点.此时,这辆越野车穿越这片沙漠的最大行程是多少![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是等边△ABC内一点,D是△ABC外的一点,∠AOB=110°,∠BOC=α,△BOC≌△ADC,∠OCD=60°,连接OD.
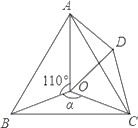
(1)求证:△OCD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当α为多少度时,△AOD是等腰三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com