
����Ŀ���Ķ�������ϣ���ɺ�����Ŀ��
0��-360����Ľǵ����Ǻ���
�ڳ��У�����ѧϰ����ǵ����ҡ����ҡ����к������������Ǻ���������ͼ1��ʾ��ֱ��������ABC����A����ǣ���ôsinA=![]() ��cosA=
��cosA=![]() ��tanA=
��tanA=![]() ��cotA=
��cotA=![]()
Ϊ���о���Ҫ�������ٴ���һ���Ƕ����涨һ���ǵ����Ǻ��������壺
����һ�����������������Ķ�����Ϊԭ�㣬������ʼ����Ϊx���������ox������ֱ������ϵ��ͼ2�����ڽ������ձ�����ȡһ��P�����ĺ�������x����������y����P��ԭ�㣨0��0���ľ���Ϊr=![]() ��r�������ģ���Ȼ��ѽ��������Ǻ����涨Ϊ��sin��=
��r�������ģ���Ȼ��ѽ��������Ǻ����涨Ϊ��sin��=![]() ��cos��=
��cos��=![]() ��tan��=
��tan��=![]() ��cot��=
��cot��=![]()
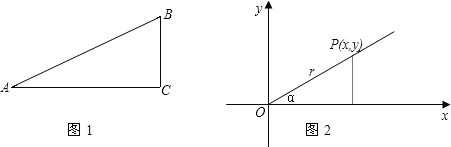
����֪����ͼ1���ĸ���ֵ�Ĵ�С���A�Ĵ�С�йأ�����ֱ�������εĴ�С�أ�ͬ��ͼ2���ĸ���ֵ�Ĵ�СҲ��������Ĵ�С�йأ������P�ڽ������ձ�λ���أ�
�Ƚ�ͼ1��ͼ2�����Կ���һ���ǵ����Ǻ�������������ֹ涨ʵ������һ���ģ����ݵڶ��ֶ���ش��������⣮
��1����90�㣼����180��������������Ǻ���ֵsin����cos����tan����cot��������ȡ��ֵ�����ļ�����
��2�����������ձ���ֱ��y=2x�غϣ���sin��+cos����ֵ��
��3���������Ƕ۽ǣ����ձ���һ��P��x��![]() ������cos��=
������cos��=![]() x����tan����ֵ��
x����tan����ֵ��
��4����0��ܦ���90������sin��+cos����ȡֵ��Χ��
���𰸡���1��sin������2��![]() ��
��![]() ����3��
����3��![]() ����4��1��sin��+cos����
����4��1��sin��+cos����![]() ��
��
��������
��1���ɵ�P��x��y���ڵڶ����ޣ��Ƴ�x��0��y��0������sin��=![]() ��cos��=
��cos��=![]() ��tan��=
��tan��=![]() ��cot��=
��cot��=![]() �������жϣ�
�������жϣ�
��2���������������ۼ��ɽ�����⣻
��3����ͼ2�У���PE��x����E����취���OE�ij����������Ǻ����Ķ��弴�ɽ�����⣻
��4������=0����90��ʱ���õ�sin��+cos������Сֵsin��+cos��=1������=45��ʱ���õ�sin��+cos�������ֵ��sin��+cos��=![]() ���ɴ˼��ɽ������.
���ɴ˼��ɽ������.
��1���ߵ�P��x��y���ڵڶ����ޣ�
��x��0��y��0��
��sin��=![]() ��cos��=
��cos��=![]() ��tan��=
��tan��=![]() ��cot��=
��cot��=![]() ��
��
��sin����0��cos����0��tan����0��cot����0��
��ȡȡ��ֵ����sin����
��2����ͼ1�У�
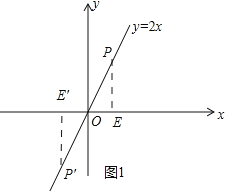
�ٵ���P�ڵ�һ����ʱ����PE��x����E����OE=a����PE=2a��OP=![]() a��
a��
��sin��+cos��=![]() ��
��
�ڵ���P�ڵ�������ʱ����PE��x����E����OE=a����PE=2a��OP=![]() a��
a��
��sin��+cos��=![]() ��
��
����������sin��+cos��=![]() ��
��![]() ��
��
��3����ͼ2�У���PE��x����E��
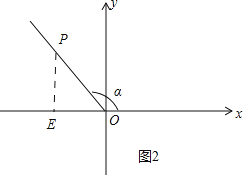
������PE=![]() ��cos��=
��cos��=![]() ��
��
��OP=2![]() ��
��
��OE=![]() ��
��
��tan��=![]() ��
��
��4������=0����90��ʱ���õ�sin��+cos������Сֵsin��+cos��=1��
����=45��ʱ���õ�sin��+cos�������ֵ��sin��+cos��=![]() ��
��
��1��sin��+cos����![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1���ⷽ�̣�3x��x��1��=2��2x��
��2����֪���κ�����ͼ����A����1��4��Ϊ�����ҹ���B��2����5������ú����Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
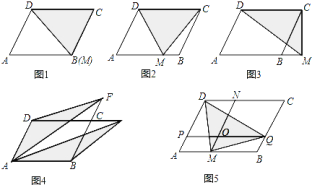
����Ŀ������̽������֪ƽ���ı���![]() �����Ϊ
�����Ϊ![]() ��
��![]() ��
��![]() ����ֱ����һ�㣮
����ֱ����һ�㣮
![]() ��ͼ
��ͼ![]() ������
������![]() ��
��![]() �غ�ʱ��
�غ�ʱ��![]() ________��
________��
![]() ��ͼ
��ͼ![]() ������
������![]() ��
��![]() ��
��![]() �����غ�ʱ��
�����غ�ʱ��![]() ________��
________��
![]() ��ͼ
��ͼ![]() ������
������![]() ��
��![]() ����
����![]() �����ӳ���ʱ��
�����ӳ���ʱ��![]() ________��
________��
��չ�ƹ㣺��ͼ![]() ��ƽ���ı���
��ƽ���ı���![]() �����Ϊ
�����Ϊ![]() ��
��![]() ��
��![]() �ֱ�Ϊ
�ֱ�Ϊ![]() ��
��![]() �ӳ��������㣬����
�ӳ��������㣬����![]() ��
��![]() ��
��![]() ��
��![]() �����ͼ����Ӱ���ֵ��������˵�����ɣ�
�����ͼ����Ӱ���ֵ��������˵�����ɣ�
ʵ��Ӧ�ã���ͼ��һƽ���ı����̵�![]() ��
��![]() ��
��![]() �ֱ�ƽ����
�ֱ�ƽ����![]() ��
��![]() �������ཻ�ڵ�
�������ཻ�ڵ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ���ֽ����̵ظ��죬���̵��ڲ���һ������������
���ֽ����̵ظ��죬���̵��ڲ���һ������������![]() ������
������![]() ��
��![]() ��
��![]() ��ͼ����Ӱ���֣���ֲ��ͬ�Ļ��ݣ��������������������
��ͼ����Ӱ���֣���ֲ��ͬ�Ļ��ݣ��������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��A��1��0����B��1��a��0����C��1+a��0����a��0������P����D��4��4��ΪԲ�ģ�1Ϊ�뾶��Բ���˶�����ʼ�������BPC=90�㣬��a�����ֵ�ǣ� ��
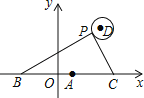
A. 3 B. 4 C. 5 D. 6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У�����A��AE��BC������ΪE������DE��FΪ�߶�DE��һ�㣬����AFE=��B

��1����֤����ADF�ס�DEC��
��2����AB=8��AD=6![]() ��AF=4
��AF=4![]() ����AE�ij���
����AE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�E��F�ֱ����߶�BC��AD���е㣬AB=2��AD=4������P��EC��CD��DF��·���ɵ�E�˶�����F�����PAB�����s�Ƕ���P�˶���·���ܳ�x�ĺ�������������Ĵ���ͼ�������
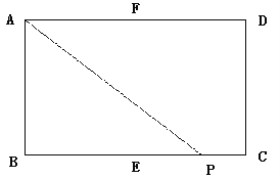
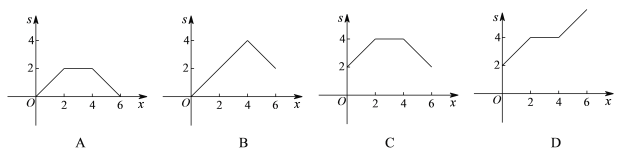
A. A B. B C. C D. D
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУΪ���˽�����������������涨�μӲ��Ե�ÿ����������ʵ����������������Զ���������������������;���1000�����ĸ���Ŀ�������ȡһ����Ϊ������Ŀ��
��1�����꣨1�����25�����������μӣ��μӸ��������Ŀ��ͳ�ƽ����ͼ���μ���ʵ���������Ե������������� ���ˣ�
��2�����꣨1������8�������μ�����������Զ���IJ��ԣ����ǵijɼ�����λ���֣����£�95��100��82��90��89��90��90��85
����95��100��82��90��89��90��90��85���������ݵ��������� ������λ������ ����
��С��ͬѧ�ijɼ���92�֣����ijɼ���Σ�
�������������90�ֵijɼ���Ϊ���㣬������ư��꼶80����������������Զ���ɼ�Ϊ�����ѧ��ԼΪ�����ˣ�
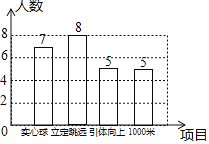
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
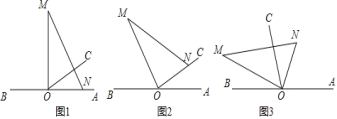
����Ŀ����ͼ1��OΪֱ��AB��һ�㣬����O������OC��![]() ����һֱ�����ǰ�
����һֱ�����ǰ�![]() ��ֱ�Ƕ�����ڵ�O����һ��ON������OA�ϣ���һ��OM��OC����ֱ��AB���Ϸ���
��ֱ�Ƕ�����ڵ�O����һ��ON������OA�ϣ���һ��OM��OC����ֱ��AB���Ϸ���
��1����ͼ1�е����ǰ��Ƶ�O��ÿ��![]() ���ٶ�����ʱ�뷽����תһ����ͼ2������t���ON����OC���ϣ���
���ٶ�����ʱ�뷽����תһ����ͼ2������t���ON����OC���ϣ���![]() ______��(ֱ��д���)��
______��(ֱ��д���)��
��2����ͼ2�����ǰ�����Ƶ�O��ÿ��![]() ���ٶ�����ʱ�뷽����ת�����OA��ͬʱ����OCҲ��O����ÿ��
���ٶ�����ʱ�뷽����ת�����OA��ͬʱ����OCҲ��O����ÿ��![]() ���ٶ�����ʱ�뷽����תһ�ܣ�
���ٶ�����ʱ�뷽����תһ�ܣ�
�ٵ�OCת��9��ʱ����![]() �Ķ�����
�Ķ�����
���˶�������ʱ��![]() ����˵�����ɣ�
����˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com