
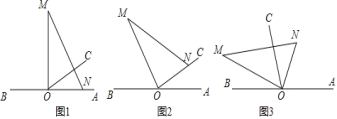
����Ŀ����ͼ1��OΪֱ��AB��һ�㣬����O������OC��![]() ����һֱ�����ǰ�
����һֱ�����ǰ�![]() ��ֱ�Ƕ�����ڵ�O����һ��ON������OA�ϣ���һ��OM��OC����ֱ��AB���Ϸ���
��ֱ�Ƕ�����ڵ�O����һ��ON������OA�ϣ���һ��OM��OC����ֱ��AB���Ϸ���
��1����ͼ1�е����ǰ��Ƶ�O��ÿ��![]() ���ٶ�����ʱ�뷽����תһ����ͼ2������t���ON����OC���ϣ���
���ٶ�����ʱ�뷽����תһ����ͼ2������t���ON����OC���ϣ���![]() ______��(ֱ��д���)��
______��(ֱ��д���)��
��2����ͼ2�����ǰ�����Ƶ�O��ÿ��![]() ���ٶ�����ʱ�뷽����ת�����OA��ͬʱ����OCҲ��O����ÿ��
���ٶ�����ʱ�뷽����ת�����OA��ͬʱ����OCҲ��O����ÿ��![]() ���ٶ�����ʱ�뷽����תһ�ܣ�
���ٶ�����ʱ�뷽����תһ�ܣ�
�ٵ�OCת��9��ʱ����![]() �Ķ�����
�Ķ�����
���˶�������ʱ��![]() ����˵�����ɣ�
����˵�����ɣ�
���𰸡���1��6����2����45������11���25��.
��������
��1����Ϊ��AOC=30��������ON����OC����ʱ�����ǰ���ת��30������תʱ���Ϊ6s��
��2����������ת�����У����Կ�������һ����������������⣬����ON�Ƶ�O��ÿ��5�����ٶ�����ʱ�뷽����ת��ͬʱ����OCҲ��O����ÿ��10�����ٶ�����ʱ�뷽����ת��
��9��ʱ����NOC=45������OC��ת��90�������ԡ�MOC�Ķ�������45����
�ڡ�MOC=35��ʱ��Ӧ��OC��OM�غ�ǰ35�����غϺ�35������������ǣ��õ�����ʱ��������Ҫ��.
��1���ߡ�AOC=30��
�����ǰ�ÿ����ת5��
�൱ON����OC����ʱ����5t=30��
��t=6
�ʴ�Ϊ��6��
��2���ٵ�OCת��9��ʱ����COA=30��+10���9=120��
����MOA=30��+90��+5���9=165��
�֡ߡ�MOC=��MOA-��COA
������MOC=165��-120��=45��
�𣺵�OCת��9��ʱ����MOC�Ķ���Ϊ45����
����OC�˶���ʼλ��Ϊ����OP����ͼ1�����˶�t��ʱ����MOC=35����
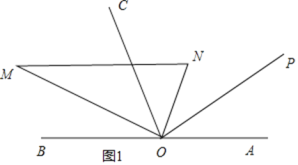
���MOP=90��+5t����COP=10t
����MOC=35��ʱ���У�90��+5t��-10t=35����10t-��90��+5t��=35��
��t=11��t=25
��Ϊ���ǰ�������OC��ֻ��תһ�ܣ����Բ������ٴ����������
�ʵ��˶�11���25��ʱ����MOC=35����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
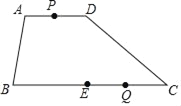
����Ŀ����ͼ�����ı���ABCD�У�AD��BC��AD=4��BC=12����E��BC���е㣮��P��Q�ֱ��DZ�AD��BC�ϵ����㣬���е�P��ÿ���1��λ���ȵ��ٶȴӵ�A�˶�����D���ٷ��ص�A��ͬʱ��Q��ÿ��2����λ���ȵ��ٶȴӵ�C�������B�˶���������һ�㵽���յ�ʱֹͣ�˶������˶�ʱ��tΪ_____��ʱ���Ե�A��P��Q��EΪ������ı�����ƽ���ı��Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������ϣ���ɺ�����Ŀ��
0��-360����Ľǵ����Ǻ���
�ڳ��У�����ѧϰ����ǵ����ҡ����ҡ����к������������Ǻ���������ͼ1��ʾ��ֱ��������ABC����A����ǣ���ôsinA=![]() ��cosA=
��cosA=![]() ��tanA=
��tanA=![]() ��cotA=
��cotA=![]()
Ϊ���о���Ҫ�������ٴ���һ���Ƕ����涨һ���ǵ����Ǻ��������壺
����һ�����������������Ķ�����Ϊԭ�㣬������ʼ����Ϊx���������ox������ֱ������ϵ��ͼ2�����ڽ������ձ�����ȡһ��P�����ĺ�������x����������y����P��ԭ�㣨0��0���ľ���Ϊr=![]() ��r�������ģ���Ȼ��ѽ��������Ǻ����涨Ϊ��sin��=
��r�������ģ���Ȼ��ѽ��������Ǻ����涨Ϊ��sin��=![]() ��cos��=
��cos��=![]() ��tan��=
��tan��=![]() ��cot��=
��cot��=![]()
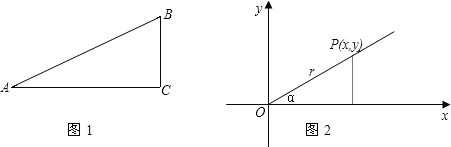
����֪����ͼ1���ĸ���ֵ�Ĵ�С���A�Ĵ�С�йأ�����ֱ�������εĴ�С�أ�ͬ��ͼ2���ĸ���ֵ�Ĵ�СҲ��������Ĵ�С�йأ������P�ڽ������ձ�λ���أ�
�Ƚ�ͼ1��ͼ2�����Կ���һ���ǵ����Ǻ�������������ֹ涨ʵ������һ���ģ����ݵڶ��ֶ���ش��������⣮
��1����90�㣼����180��������������Ǻ���ֵsin����cos����tan����cot��������ȡ��ֵ�����ļ�����
��2�����������ձ���ֱ��y=2x�غϣ���sin��+cos����ֵ��
��3���������Ƕ۽ǣ����ձ���һ��P��x��![]() ������cos��=
������cos��=![]() x����tan����ֵ��
x����tan����ֵ��
��4����0��ܦ���90������sin��+cos����ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ������ϵxOy�У�һ�κ���y=��![]() x+5��ͼ��l1�ֱ���x��y�ύ��A��B���㣬������������ͼ��l2��l1���ڵ�C��m��4����
x+5��ͼ��l1�ֱ���x��y�ύ��A��B���㣬������������ͼ��l2��l1���ڵ�C��m��4����
��1����m��ֵ��l2�Ľ���ʽ��
��2����S��AOC��S��BOC��ֵ��
��3��һ�κ���y=kx+1��ͼ��Ϊl3����11��l2��l3����Χ�������Σ�ֱ��д��k��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������������У���ABC�����㶼�ڸ���ϣ���A��C������ֱ�Ϊ����5��1��������1��4�������������ƽ��ֱ������ϵ����������⣺
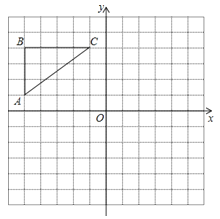
��1��������ABC����y��ԳƵ���A1B1C1��
��2��������ABC����ԭ��O�ԳƵ���A2B2C2��
��3����C1�������� ����C2�������� ��
��4�����жϣ�![]() ��
��![]() �Ƿ����x��Գ�?��ֻ��д���жϽ���� ��
�Ƿ����x��Գ�?��ֻ��д���жϽ���� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
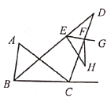
����Ŀ����ͼ��![]() ��
��![]() ��ƽ������
��ƽ������![]() �����ƽ�����ཻ�ڵ�
�����ƽ�����ཻ�ڵ�![]() ����
����![]() �ֱ����߶�
�ֱ����߶�![]() ��
��![]() �ϣ���
�ϣ���![]() ��
��![]() ���ӳ����ϣ�
���ӳ����ϣ�![]() ��
��![]() ����ֱ��
����ֱ��![]() �Գƣ���
�Գƣ���![]() ����
����![]() __________.
__________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��2018��ƽ��ÿ�������������Ϊ40���/�죬2019��ƽ��ÿ��������ŷ�����2018��ƽ��ÿ��������ŷ�����100��֣�2019��ƽ��ÿ���������������2018��ƽ��ÿ���������������2. 5��. ��2019��ƽ��ÿ���������������2018��ƽ��ÿ������������ʵ�1. 25��.
��ע��![]() ��
��
��1�������2018��ƽ��ÿ��������ŷ�����
��2��Ԥ�Ƹ���2020��ƽ��ÿ��������ŷ�����2019��ƽ��ÿ��������ŷ�������![]() . ������մ���Ҫ��������ƽ��ÿ������������ʲ�����
. ������մ���Ҫ��������ƽ��ÿ������������ʲ�����![]() ������ô����2020��ƽ��ÿ���������������2019��ƽ��ÿ��������������Ļ����ϣ����ٻ���Ҫ���Ӷ�����ֲ���ʹ����2020��ƽ��ÿ������������ʷ��ϴ�����Ҫ��
������ô����2020��ƽ��ÿ���������������2019��ƽ��ÿ��������������Ļ����ϣ����ٻ���Ҫ���Ӷ�����ֲ���ʹ����2020��ƽ��ÿ������������ʷ��ϴ�����Ҫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����������30���ǵ����dz߰ڷ���һ�𣬿���֤����ABD�ǵȱ������Σ��������ǵõ�����ֱ���������У����һ����ǵ���30������ô�����Ե�ֱ�DZߵ���б�ߵ�һ��.
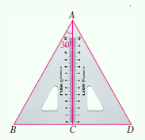

��������������ͽ��ۣ��õ���������⣺
��ֱ����ABC�У���ACB=90�㣬���![]() ����ô��BAC=30����
����ô��BAC=30����
���жϴ��������٣���Ϊ�����⣬�����֤������Ϊ�����⣬��˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ����ӵ�һ��ԽҰ����Ҫ��ԽһƬɳĮ����������ÿ��װ���������ֻ����ʻ![]() ���ӳ����һ����������ɳĮ�������ɸ����͵㣨ԽҰ����Խ��ɳĮ���Ϳ���������ͣ�.
���ӳ����һ����������ɳĮ�������ɸ����͵㣨ԽҰ����Խ��ɳĮ���Ϳ���������ͣ�.
��1�������Խȫ�̴���![]() ��ɳĮ����ɳĮ����һ�����͵�
��ɳĮ����ɳĮ����һ�����͵�![]() ��ԽҰ��װ���ʹ����
��ԽҰ��װ���ʹ����![]() �����������͵�
�����������͵�![]() ʱ�ӳ���ȡ�������ͷŽ�
ʱ�ӳ���ȡ�������ͷŽ�![]() ���͵㣬Ȼ�س����㣬�����ͺ��ٿ���
���͵㣬Ȼ�س����㣬�����ͺ��ٿ���![]() ����
����![]() ���͵�ʱ��ȡ������������ͷ��ڳ��ϣ��ٴ�
���͵�ʱ��ȡ������������ͷ��ڳ��ϣ��ٴ�![]() ���������յ㣬��ʱ������ԽҰ����Խ��ƬɳĮ������г��Ƕ���
���������յ㣬��ʱ������ԽҰ����Խ��ƬɳĮ������г��Ƕ���![]() ��
��
��2�������Խȫ�̴���![]() ��ɳĮ����ɳĮ����2�����͵�
��ɳĮ����ɳĮ����2�����͵�![]() ��
��![]() ��ԽҰ��װ���ʹ����
��ԽҰ��װ���ʹ����![]() �����������͵�
�����������͵�![]() ʱ�ӳ���ȡ�������ͷŽ�
ʱ�ӳ���ȡ�������ͷŽ�![]() ���͵㣻Ȼ�س�����
���͵㣻Ȼ�س�����![]() �����ͣ������͵�
�����ͣ������͵�![]() ʱȡ�����͵�
ʱȡ�����͵�![]() ��ȫ���ͷŵ����ϣ��ٵ��ﴢ�͵�
��ȫ���ͷŵ����ϣ��ٵ��ﴢ�͵�![]() ���ӳ���ȡ�������ͷŽ�
���ӳ���ȡ�������ͷŽ�![]() ���͵㣻Ȼ�س�����
���͵㣻Ȼ�س�����![]() �����ͣ���
�����ͣ���![]() ���͵�ȡ������������ͷ��ڳ��ϣ�����յ�.��ʱ������ԽҰ����Խ��ƬɳĮ������г��Ƕ���
���͵�ȡ������������ͷ��ڳ��ϣ�����յ�.��ʱ������ԽҰ����Խ��ƬɳĮ������г��Ƕ���![]() ��
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com