
【题目】如图,![]() 的
的![]() 的平分线与
的平分线与![]() 的外角平分线相交于点
的外角平分线相交于点![]() ,点
,点![]() 分别在线段
分别在线段![]() 、
、![]() 上,点
上,点![]() 在
在![]() 的延长线上,
的延长线上,![]() 与
与![]() 关于直线
关于直线![]() 对称,若
对称,若![]() ,则
,则![]() __________.
__________.
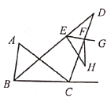
【答案】78.
【解析】
利用![]() 的
的![]() 的平分线与
的平分线与![]() 的外角平分线相交于点
的外角平分线相交于点![]() 得到∠DBC=
得到∠DBC=![]() ∠ABC,∠ACD=
∠ABC,∠ACD=![]() (∠A+∠ABC),根据三角形的内角和得到∠D=
(∠A+∠ABC),根据三角形的内角和得到∠D=![]() ∠A=30
∠A=30![]() ,利用外角定理得到∠DEH=
,利用外角定理得到∠DEH=![]() ,由
,由![]() 与
与![]() 关于直线
关于直线![]() 对称得到∠DEG=∠HEG=48
对称得到∠DEG=∠HEG=48![]() ,根据外角定理即可得到∠DFG=∠D+∠DEG=78
,根据外角定理即可得到∠DFG=∠D+∠DEG=78![]() .
.
∵![]() 的
的![]() 的平分线与
的平分线与![]() 的外角平分线相交于点
的外角平分线相交于点![]()
∴∠DBC=![]() ∠ABC,∠ACD=
∠ABC,∠ACD=![]() (∠A+∠ABC),
(∠A+∠ABC),
∵∠DBC+∠BCD+∠D=180![]() ,∠A+∠ABC+∠ACB=180
,∠A+∠ABC+∠ACB=180![]() ,
,
∴∠D=![]() ∠A=30
∠A=30![]() ,
,
∵![]() ,
,
∴∠DEH=![]() ,
,
∵![]() 与
与![]() 关于直线
关于直线![]() 对称,
对称,
∴∠DEG=∠HEG=48![]() ,∠DFG=∠HFG
,∠DFG=∠HFG![]() ,
,
∵∠DFG=∠D+∠DEG=78![]() ,
,
∴n=78.
故答案为:78.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E,F分别是线段BC,AD的中点,AB=2,AD=4,动点P沿EC,CD,DF的路线由点E运动到点F,则△PAB的面积s是动点P运动的路径总长x的函数,这个函数的大致图象可能是
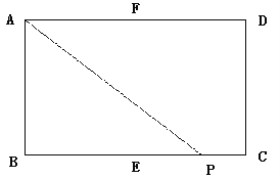
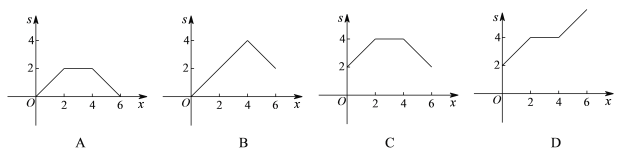
A. A B. B C. C D. D
查看答案和解析>>
科目:初中数学 来源: 题型:
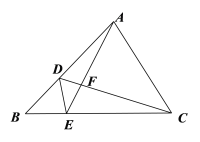
【题目】已知:如图,在△ABC中,点D,E分别在边AB,BC上,BABD=BCBE
(1)求证:△BDE∽△BCA;
(2)如果AE=AC,求证:AC2=ADAB.
查看答案和解析>>
科目:初中数学 来源: 题型:
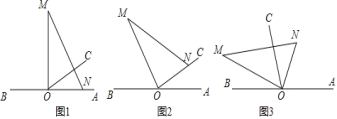
【题目】如图1,O为直线AB上一点,过点O作射线OC,![]() ,将一直角三角板
,将一直角三角板![]() 的直角顶点放在点O处,一边ON在射线OA上,另一边OM与OC都在直线AB的上方.
的直角顶点放在点O处,一边ON在射线OA上,另一边OM与OC都在直线AB的上方.
(1)将图1中的三角板绕点O以每秒![]() 的速度沿逆时针方向旋转一周如图2,经过t秒后,ON落在OC边上,则
的速度沿逆时针方向旋转一周如图2,经过t秒后,ON落在OC边上,则![]() ______秒(直接写结果).
______秒(直接写结果).
(2)如图2,三角板继续绕点O以每秒![]() 的速度沿逆时针方向旋转到起点OA上同时射线OC也绕O点以每秒
的速度沿逆时针方向旋转到起点OA上同时射线OC也绕O点以每秒![]() 的速度沿逆时针方向旋转一周,
的速度沿逆时针方向旋转一周,
①当OC转动9秒时,求![]() 的度数.
的度数.
②运动多少秒时,![]() ?请说明理由.
?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
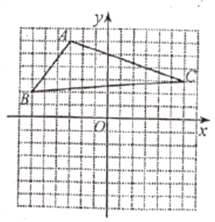
【题目】如图,![]() 的三个顶点的坐标分别为
的三个顶点的坐标分别为![]() 、
、![]() 、
、![]() .
. ![]() 与
与![]() 关于
关于![]() 轴对称,
轴对称,![]() 与
与![]() 关于
关于![]() 轴对称,点
轴对称,点![]() 、
、![]() 、
、![]() 分别是点
分别是点![]() 、
、![]() 、
、![]() 的对应点,点
的对应点,点![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 的对应点.
的对应点.
(1)画出![]() 与
与![]() ,并写出点
,并写出点![]() 、
、![]() 、
、![]() 的坐标;
的坐标;
(2)连接![]() 、
、![]() ,求六边形
,求六边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了落实国务院副总理李克强同志到恩施考察时的指示精神,最近,州委州政府又出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农副产品,已知这种产品的成本价为20元/千克.市场调查发现,该产品每天的销售量w(千克)与销售价x(元/千克)有如下关系:w=-2x+80.设这种产品每天的销售利润为y(元).
(1)求y与x之间的函数关系式.
(2)当销售价定为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果物价部门规定这种产品的销售价不得高于28元/千克,该农户想要每天获得150元的销售利润,销售价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
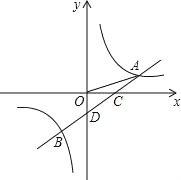
【题目】如图,一次函数y=ax+b的图象与反比例函数![]() 的图象交于A,B两点,与X轴交于点C,与Y轴交于点D,已知
的图象交于A,B两点,与X轴交于点C,与Y轴交于点D,已知![]() ,A(n,1),点B的坐标为(﹣2,m)
,A(n,1),点B的坐标为(﹣2,m)
(1)求反比例函数的解析式和一次函数的解析式;
(2)连结BO,求△AOB的面积;
(3)观察图象直接写出一次函数的值大于反比例函数的值时x的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小微企业为加快产业转型升级步伐,引进一批A,B两种型号的机器.已知一台A型机器比一台B型机器每小时多加工2个零件,且一台A型机器加工80个零件与一台B型机器加工60个零件所用时间相等.
(1)每台A,B两种型号的机器每小时分别加工多少个零件?
(2)如果该企业计划安排A,B两种型号的机器共10台一起加工一批该零件,为了如期完成任务,要求两种机器每小时加工的零件不少于72件,同时为了保障机器的正常运转,两种机器每小时加工的零件不能超过76件,那么A,B两种型号的机器可以各安排多少台?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com