
【题目】在平面直角坐标系中,设二次函数y1=mx2﹣6mx+8m(m为常数).
(1)若函数y1经过点(1,3),求函数y1的表达式;
(2)若m<0,当x<![]() 时,此二次函数y随x的增大而增大,求a的取值范围;
时,此二次函数y随x的增大而增大,求a的取值范围;
(3)已知一次函数y2=x﹣2,当y1y2>0时,求x的取值范围.
【答案】(1)y1=x2﹣6x+8;(2)a≤6;(3)当m>0时,x>4;当m<0时,x<4且x≠2.
【解析】
(1)把已知点坐标代入即可确定出所求;
(2)求出抛物线的对称轴,根据m小于0得到抛物线开口向下,利用二次函数增减性确定出a的范围即可;
(3)把各自的解析式代入已知不等式,分类讨论m的范围即可确定出x的范围.
(1)把(1,3)代入y1=mx2﹣6mx+8m,得:m=1,则y1=x2﹣6x+8;
(2)∵抛物线的对称轴为直线x=![]() =3,m<0,∴抛物线开口向下,当x≤3时,二次函数y随x的增大而增大,由x<
=3,m<0,∴抛物线开口向下,当x≤3时,二次函数y随x的增大而增大,由x<![]() 时,此二次函数y随x的增大而增大,得到:
时,此二次函数y随x的增大而增大,得到:![]() ≤3,即a≤6;
≤3,即a≤6;
(3)由题意得:y1y2=(mx2﹣6mx+8m)(x﹣2)=m(x2﹣6x+8)(x﹣2)=m(x﹣2)2(x﹣4)>0.当x≠2时,(x﹣2)2>0,∴当m>0时,x>4;当m<0时,x<4且x≠2.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:
【题目】.Rt△ABC中,已知∠C=90°,∠B=50°,点D在边BC上,BD=2CD(图4).把△ABC绕着点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m=_________![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
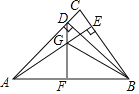
【题目】在△ABC中,∠CAB=45°,BD⊥AC于点D,AE⊥BC于点E,DF⊥AB于点F,AE与DF交于点G,连接BG.
(1)求证:AG=BG;
(2)已知AG=5,BE=4,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县教育行政部门为了了解八年级学生每学期参加综合实践活动的情况,随机抽样调查了该县八年级学生一个学期参加综合实践活动的天数,并用得到的数据绘制了下面两幅不完整的统计图(如图).
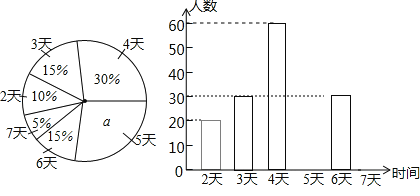
请你根据图中提供的信息,回答下列问题:
(1)求出参加抽样调查的八年级学生人数,并将频数直方图补充完整.
(2)在这次抽样调查中,众数和中位数分别是多少?
(3)如果该县共有八年级学生![]() 人,请你估计“活动时间不少于
人,请你估计“活动时间不少于![]() 天”的大约有多少人?
天”的大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知![]() ,
,![]() 是平面上的任意一点,过点
是平面上的任意一点,过点![]() 作
作![]() ,
,![]() ,垂足分别为点
,垂足分别为点![]() 、
、![]() ,求
,求![]() 的度数.
的度数.
(2)探究![]() 与
与![]() 有什么关系?(直接写出结论)
有什么关系?(直接写出结论)
(3)通过上面这两道题,你能说出如果一个角的两边分别垂直于另一个角的两边,则这两个角是什么关系吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
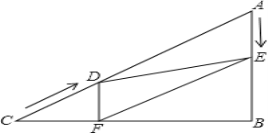
【题目】如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个动点到达终点时,另一个动点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
(1)当t为何值时,DF=DA?
(2)当t为何值时,△ADE为直角三角形?请说明理由.
(3)是否存在某一时刻t,使点F在线段AC的中垂线上,若存在,请求出t值,若不存在,请说明理由.
(4)请用含有t式子表示△DEF的面积,并判断是否存在某一时刻t,使△DEF的面积是△ABC面积的![]() ,若存在,请求出t值,若不存在,请说明理由.
,若存在,请求出t值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
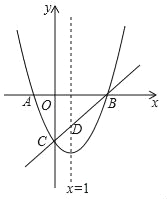
【题目】如图,已知抛物线y=x2+bx+c与x轴交于A、B(点A在点B的左侧),与y轴交于点C(0,﹣3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D.
(1)求抛物线的函数解析式;
(2)求直线BC的函数解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com